题目
求函数=(e)^cos x+arctan sqrt (x)的导数
求函数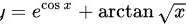 的导数
的导数
题目解答
答案
根据复合函数求导法则,得出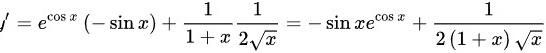
解析
步骤 1:求导数
首先,我们对函数$y={e}^{\cos x}+\arctan \sqrt {x}$进行求导。根据求导法则,我们需要分别对每一项进行求导。
步骤 2:对${e}^{\cos x}$求导
对于${e}^{\cos x}$,我们使用链式法则。设$u=\cos x$,则$y={e}^{u}$。根据链式法则,$y'={e}^{u}u'$。因为$u'=-\sin x$,所以${e}^{\cos x}$的导数为$-{e}^{\cos x}\sin x$。
步骤 3:对$\arctan \sqrt {x}$求导
对于$\arctan \sqrt {x}$,我们同样使用链式法则。设$v=\sqrt {x}$,则$y=\arctan v$。根据链式法则,$y'=\dfrac {1}{1+v^{2}}v'$。因为$v'=\dfrac {1}{2\sqrt {x}}$,所以$\arctan \sqrt {x}$的导数为$\dfrac {1}{1+(\sqrt {x})^{2}}\cdot \dfrac {1}{2\sqrt {x}}=\dfrac {1}{2(1+x)\sqrt {x}}$。
步骤 4:合并结果
将上述两部分的结果合并,得到$y$的导数为$y'=-{e}^{\cos x}\sin x+\dfrac {1}{2(1+x)\sqrt {x}}$。
首先,我们对函数$y={e}^{\cos x}+\arctan \sqrt {x}$进行求导。根据求导法则,我们需要分别对每一项进行求导。
步骤 2:对${e}^{\cos x}$求导
对于${e}^{\cos x}$,我们使用链式法则。设$u=\cos x$,则$y={e}^{u}$。根据链式法则,$y'={e}^{u}u'$。因为$u'=-\sin x$,所以${e}^{\cos x}$的导数为$-{e}^{\cos x}\sin x$。
步骤 3:对$\arctan \sqrt {x}$求导
对于$\arctan \sqrt {x}$,我们同样使用链式法则。设$v=\sqrt {x}$,则$y=\arctan v$。根据链式法则,$y'=\dfrac {1}{1+v^{2}}v'$。因为$v'=\dfrac {1}{2\sqrt {x}}$,所以$\arctan \sqrt {x}$的导数为$\dfrac {1}{1+(\sqrt {x})^{2}}\cdot \dfrac {1}{2\sqrt {x}}=\dfrac {1}{2(1+x)\sqrt {x}}$。
步骤 4:合并结果
将上述两部分的结果合并,得到$y$的导数为$y'=-{e}^{\cos x}\sin x+\dfrac {1}{2(1+x)\sqrt {x}}$。