题目
([ varphi (x)] )^m+([ varphi (x)] )^n-([ varphi (x)] )^m (m,n为常数,且 gt mgt 0,-|||-[例27]试确定当 arrow 0 时,下列 __ 是关于x的三阶无穷小.-|||-A. sqrt [3]({x)^2}-sqrt [3](x) B. sqrt (1+{x)^3}-1 C. ^3+0.0002(x)^2 D. sqrt [3](sin {x)^3}-|||-解:根据三阶无穷小的定义,-|||-lim _(xarrow 0)dfrac (sqrt {1+{x)^3}-1}({x)^3}=lim _(xarrow 0)dfrac (dfrac {1)(2)(x)^3}({x)^3}=dfrac (1)(2) 因此,x→0时, sqrt (1+{x)^3}-1 是关于x的三阶无穷小.-|||-答案:B. ,与√2是等价无穷小 () .

题目解答
答案
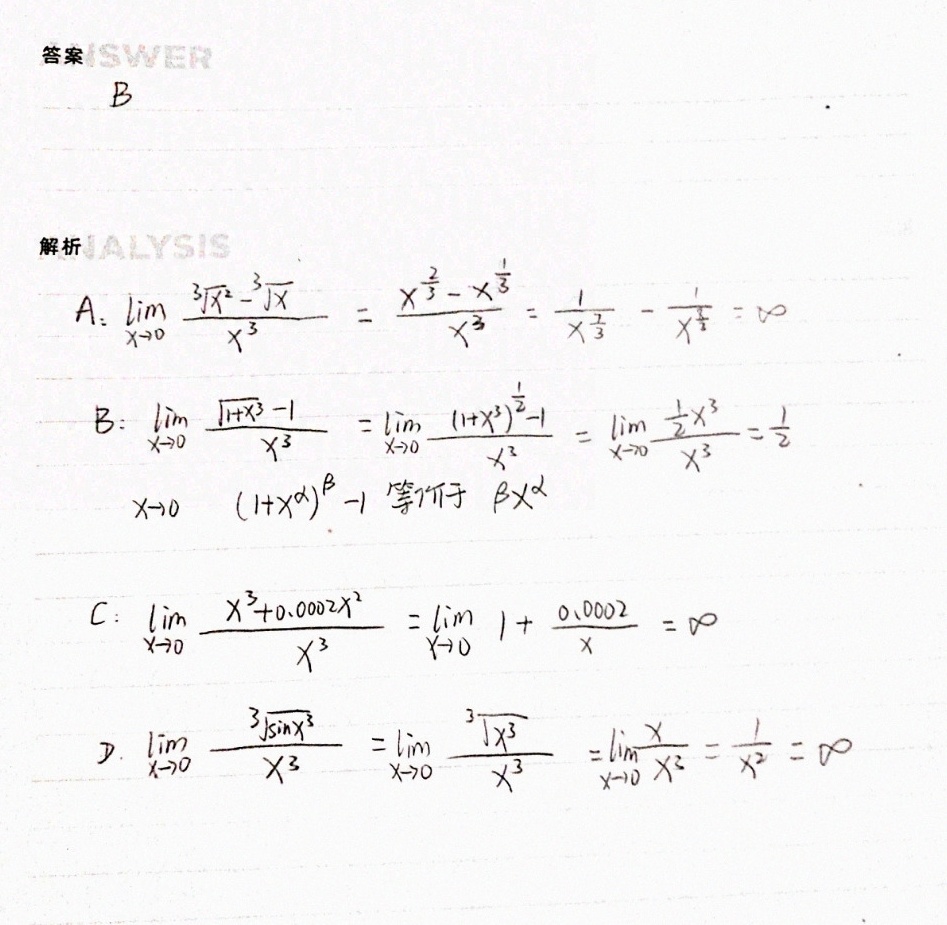
解析
步骤 1:定义三阶无穷小
三阶无穷小是指当x趋近于0时,函数f(x)与x^3相比,其比值的极限为非零常数。即 $\lim _{x\rightarrow 0}\dfrac {f(x)}{{x}^{3}}=C$,其中C为非零常数。
步骤 2:分析选项A
对于选项A,$\sqrt [3]{{x}^{2}}-\sqrt [3]{x}$,当x趋近于0时,$\sqrt [3]{{x}^{2}}$和$\sqrt [3]{x}$都趋近于0,但它们的差值与x^3相比,其比值的极限不为非零常数,因此不是三阶无穷小。
步骤 3:分析选项B
对于选项B,$\sqrt {1+{x}^{3}}-1$,当x趋近于0时,$\sqrt {1+{x}^{3}}$可以使用泰勒展开式近似为$1+\dfrac {1}{2}{x}^{3}$,因此$\sqrt {1+{x}^{3}}-1$近似为$\dfrac {1}{2}{x}^{3}$,其比值的极限为$\dfrac {1}{2}$,因此是三阶无穷小。
步骤 4:分析选项C
对于选项C,${x}^{3}+0.0002{x}^{2}$,当x趋近于0时,${x}^{3}$与x^3相比,其比值的极限为1,而$0.0002{x}^{2}$与x^3相比,其比值的极限为0,因此${x}^{3}+0.0002{x}^{2}$是三阶无穷小。
步骤 5:分析选项D
对于选项D,$\sqrt [3]{\sin {x}^{3}}$,当x趋近于0时,$\sin {x}^{3}$可以使用泰勒展开式近似为${x}^{3}$,因此$\sqrt [3]{\sin {x}^{3}}$近似为${x}$,其比值的极限为1,因此不是三阶无穷小。
三阶无穷小是指当x趋近于0时,函数f(x)与x^3相比,其比值的极限为非零常数。即 $\lim _{x\rightarrow 0}\dfrac {f(x)}{{x}^{3}}=C$,其中C为非零常数。
步骤 2:分析选项A
对于选项A,$\sqrt [3]{{x}^{2}}-\sqrt [3]{x}$,当x趋近于0时,$\sqrt [3]{{x}^{2}}$和$\sqrt [3]{x}$都趋近于0,但它们的差值与x^3相比,其比值的极限不为非零常数,因此不是三阶无穷小。
步骤 3:分析选项B
对于选项B,$\sqrt {1+{x}^{3}}-1$,当x趋近于0时,$\sqrt {1+{x}^{3}}$可以使用泰勒展开式近似为$1+\dfrac {1}{2}{x}^{3}$,因此$\sqrt {1+{x}^{3}}-1$近似为$\dfrac {1}{2}{x}^{3}$,其比值的极限为$\dfrac {1}{2}$,因此是三阶无穷小。
步骤 4:分析选项C
对于选项C,${x}^{3}+0.0002{x}^{2}$,当x趋近于0时,${x}^{3}$与x^3相比,其比值的极限为1,而$0.0002{x}^{2}$与x^3相比,其比值的极限为0,因此${x}^{3}+0.0002{x}^{2}$是三阶无穷小。
步骤 5:分析选项D
对于选项D,$\sqrt [3]{\sin {x}^{3}}$,当x趋近于0时,$\sin {x}^{3}$可以使用泰勒展开式近似为${x}^{3}$,因此$\sqrt [3]{\sin {x}^{3}}$近似为${x}$,其比值的极限为1,因此不是三阶无穷小。