3.求极限 lim _(xarrow 1)dfrac (sqrt [3]{x)-1}(sqrt {x)-1}
题目解答
答案
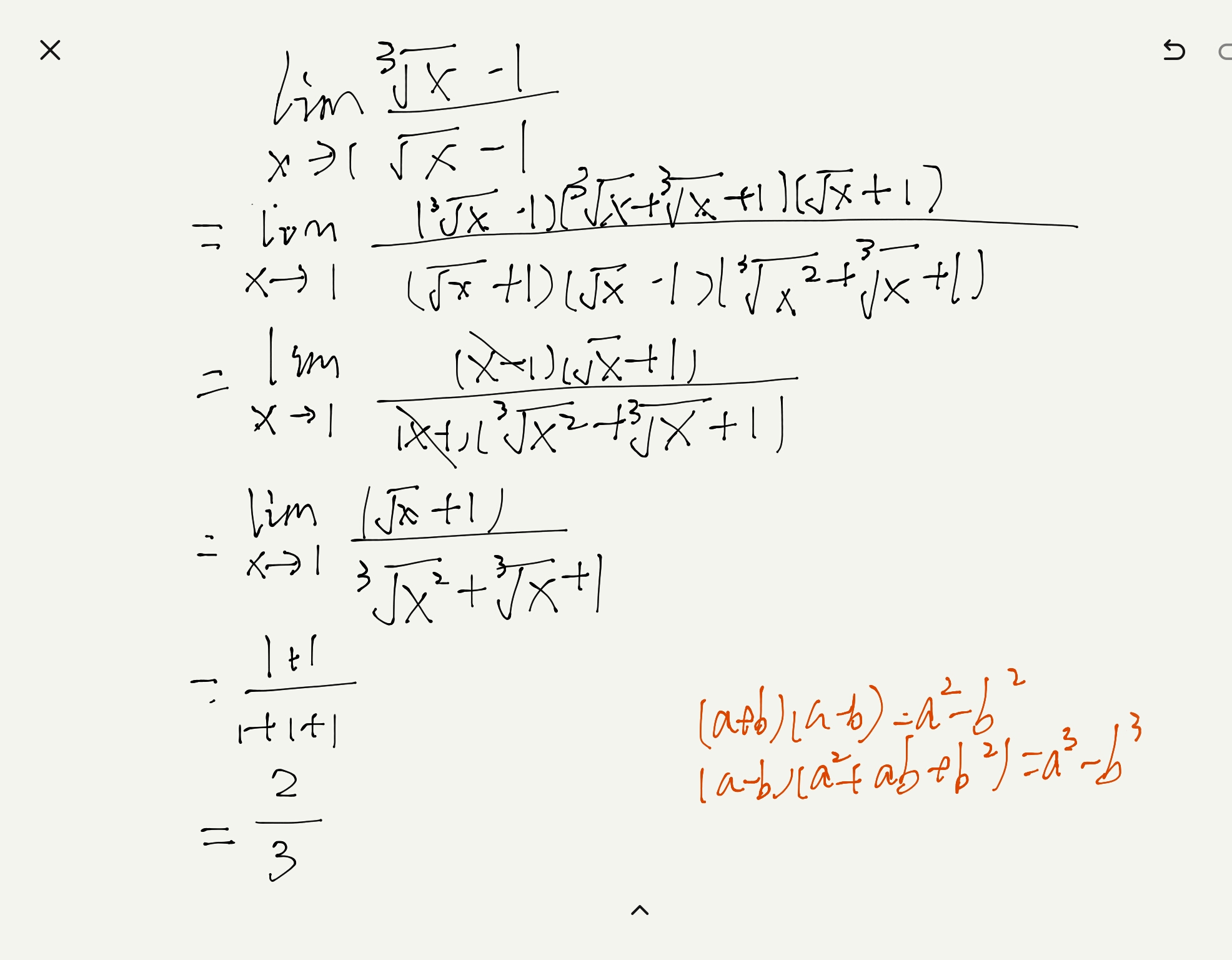
解析
考查要点:本题主要考查0/0型不定式的极限求解方法,涉及根式的有理化处理或洛必达法则的应用。
解题核心思路:
当直接代入$x=1$导致分子分母均为0时,需通过变形消除不定式。
关键方法:
- 代数变形法:将分子分母分别有理化,约分后直接代入求极限。
- 洛必达法则:对分子分母分别求导,简化表达式后求极限。
方法一:代数变形法
步骤1:有理化分子
分子$\sqrt[3]{x} - 1$可视为$a^3 - b^3$的形式,利用立方差公式:
$\sqrt[3]{x} - 1 = \frac{x - 1}{(\sqrt[3]{x})^2 + \sqrt[3]{x} + 1} = \frac{x - 1}{x^{2/3} + x^{1/3} + 1}.$
步骤2:有理化分母
分母$\sqrt{x} - 1$可视为$a^2 - b^2$的形式,利用平方差公式:
$\sqrt{x} - 1 = \frac{x - 1}{\sqrt{x} + 1}.$
步骤3:代入原式并约分
原式变形为:
$\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} = \frac{\frac{x - 1}{x^{2/3} + x^{1/3} + 1}}{\frac{x - 1}{\sqrt{x} + 1}} = \frac{\sqrt{x} + 1}{x^{2/3} + x^{1/3} + 1}.$
步骤4:代入$x=1$求极限
当$x \to 1$时,$\sqrt{x} \to 1$,$x^{2/3} \to 1$,因此:
$\lim_{x \to 1} \frac{\sqrt{x} + 1}{x^{2/3} + x^{1/3} + 1} = \frac{1 + 1}{1 + 1 + 1} = \frac{2}{3}.$
方法二:洛必达法则
步骤1:验证条件
当$x \to 1$时,分子$\sqrt[3]{x} - 1 \to 0$,分母$\sqrt{x} - 1 \to 0$,满足0/0型不定式,可应用洛必达法则。
步骤2:求导分子分母
分子导数:$\frac{d}{dx} (\sqrt[3]{x} - 1) = \frac{1}{3}x^{-2/3}$,
分母导数:$\frac{d}{dx} (\sqrt{x} - 1) = \frac{1}{2}x^{-1/2}$。
步骤3:应用洛必达法则
极限变为:
$\lim_{x \to 1} \frac{\frac{1}{3}x^{-2/3}}{\frac{1}{2}x^{-1/2}} = \lim_{x \to 1} \frac{2}{3}x^{-2/3 + 1/2} = \lim_{x \to 1} \frac{2}{3}x^{-1/6}.$
步骤4:代入$x=1$
$\frac{2}{3} \cdot 1^{-1/6} = \frac{2}{3}.$