题目
[题目]在 Delta ABC 中,顶点c在AB边上的射影为D,-|||-且 ^2=ADcdot DB, 求证: Delta ABC 是直角三角形

题目解答
答案
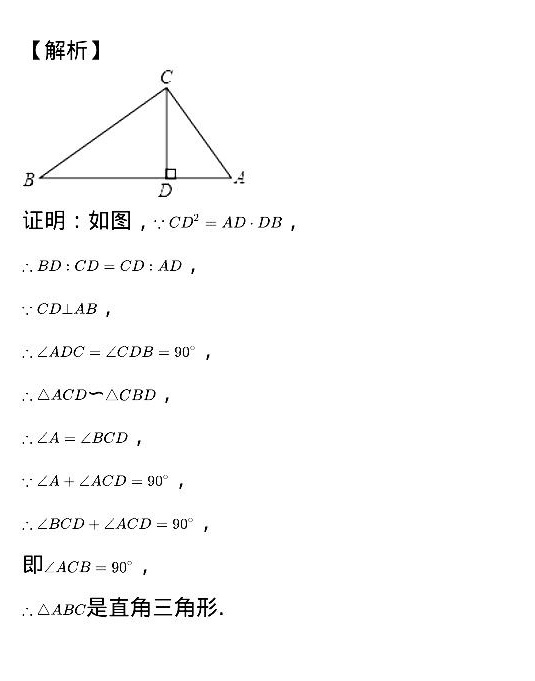
解析
考查要点:本题主要考查相似三角形的判定与性质、勾股定理的应用,以及通过比例关系推导角度关系的能力。
解题核心思路:
题目中给出的条件是$CD^2 = AD \cdot DB$,结合$CD \perp AB$,可以构造相似三角形。通过比例关系和直角条件,证明$\angle ACB = 90^\circ$,从而得出$\Delta ABC$为直角三角形。
破题关键点:
- 识别相似三角形:利用$CD^2 = AD \cdot DB$变形为比例式,结合直角条件,判定$\Delta ACD \sim \Delta BCD$。
- 角度关系转化:通过相似三角形对应角相等,推导$\angle A = \angle BCD$,并结合$\angle A + \angle ACD = 90^\circ$,最终得到$\angle ACB = 90^\circ$。
步骤1:构造比例关系
由条件$CD^2 = AD \cdot DB$,变形得:
$\frac{BD}{CD} = \frac{CD}{AD}$
步骤2:判定相似三角形
在$\Delta BCD$和$\Delta ACD$中:
- $\angle BDC = \angle ADC = 90^\circ$($CD$为$AB$的高)
- $\frac{BD}{CD} = \frac{CD}{AD}$(已证比例关系)
根据SAS相似判定定理,$\Delta BCD \sim \Delta ACD$。
步骤3:推导角度关系
由相似三角形对应角相等,得:
$\angle A = \angle BCD$
步骤4:证明$\angle ACB = 90^\circ$
在$\Delta ACD$中,$\angle A + \angle ACD = 90^\circ$。
又$\angle BCD = \angle A$,因此:
$\angle BCD + \angle ACD = 90^\circ$
即$\angle ACB = 90^\circ$,故$\Delta ABC$为直角三角形。