题目
1 lim _(xarrow 0)xcos dfrac (1)(x)=
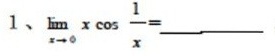
题目解答
答案

解析
步骤 1:分析函数
函数为 \( x \cos \left( \frac{1}{x} \right) \)。当 \( x \) 趋近于 0 时,\( \frac{1}{x} \) 趋向于无穷大,因此 \( \cos \left( \frac{1}{x} \right) \) 在 \([-1, 1]\) 之间振荡。
步骤 2:应用极限性质
当 \( x \) 趋近于 0 时,\( x \) 是无穷小量,而 \( \cos \left( \frac{1}{x} \right) \) 是有界函数(其值在 \([-1, 1]\) 之间)。根据极限的性质,无穷小量与有界函数的乘积仍然是无穷小量。
步骤 3:计算极限
根据上述分析,当 \( x \) 趋近于 0 时,\( x \cos \left( \frac{1}{x} \right) \) 趋向于 0。
函数为 \( x \cos \left( \frac{1}{x} \right) \)。当 \( x \) 趋近于 0 时,\( \frac{1}{x} \) 趋向于无穷大,因此 \( \cos \left( \frac{1}{x} \right) \) 在 \([-1, 1]\) 之间振荡。
步骤 2:应用极限性质
当 \( x \) 趋近于 0 时,\( x \) 是无穷小量,而 \( \cos \left( \frac{1}{x} \right) \) 是有界函数(其值在 \([-1, 1]\) 之间)。根据极限的性质,无穷小量与有界函数的乘积仍然是无穷小量。
步骤 3:计算极限
根据上述分析,当 \( x \) 趋近于 0 时,\( x \cos \left( \frac{1}{x} \right) \) 趋向于 0。