题目
设函数y=y(x)由^x-tx-(t)^2=0-|||-__-|||-arct (ty)=ln (1+(t)^2(y)^2)所确定,求^x-tx-(t)^2=0-|||-__-|||-arct (ty)=ln (1+(t)^2(y)^2)
设函数y=y(x)由
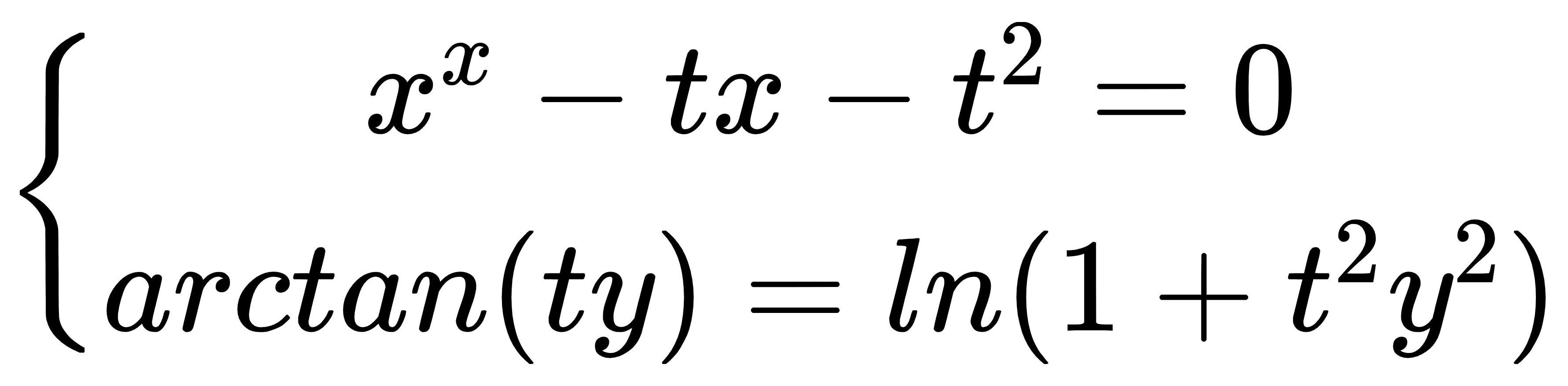
所确定,求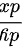
题目解答
答案
根据参数方程求导公式可知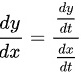
有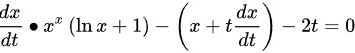
解得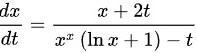
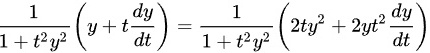
解得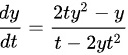
于是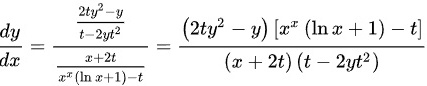
解析
步骤 1:参数方程求导
根据参数方程求导公式,我们有
$$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$$
步骤 2:求$\frac{dx}{dt}$
对$x^x - tx - t^2 = 0$关于$t$求导,得到
$$\frac{d}{dt}(x^x) - \frac{d}{dt}(tx) - \frac{d}{dt}(t^2) = 0$$
利用链式法则和乘积法则,得到
$$x^x(\ln x + 1)\frac{dx}{dt} - x - t\frac{dx}{dt} - 2t = 0$$
解得
$$\frac{dx}{dt} = \frac{x + 2t}{x^x(\ln x + 1) - t}$$
步骤 3:求$\frac{dy}{dt}$
对$\arctan(ty) = \ln(1 + t^2)$关于$t$求导,得到
$$\frac{d}{dt}(\arctan(ty)) = \frac{d}{dt}(\ln(1 + t^2))$$
利用链式法则,得到
$$\frac{1}{1 + (ty)^2}(y + t\frac{dy}{dt}) = \frac{2t}{1 + t^2}$$
解得
$$\frac{dy}{dt} = \frac{2t(1 + t^2) - y(1 + (ty)^2)}{t(1 + (ty)^2)}$$
步骤 4:求$\frac{dy}{dx}$
将$\frac{dx}{dt}$和$\frac{dy}{dt}$代入$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$,得到
$$\frac{dy}{dx} = \frac{\frac{2t(1 + t^2) - y(1 + (ty)^2)}{t(1 + (ty)^2)}}{\frac{x + 2t}{x^x(\ln x + 1) - t}}$$
化简得到
$$\frac{dy}{dx} = \frac{(2t(1 + t^2) - y(1 + (ty)^2))(x^x(\ln x + 1) - t)}{t(1 + (ty)^2)(x + 2t)}$$
根据参数方程求导公式,我们有
$$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$$
步骤 2:求$\frac{dx}{dt}$
对$x^x - tx - t^2 = 0$关于$t$求导,得到
$$\frac{d}{dt}(x^x) - \frac{d}{dt}(tx) - \frac{d}{dt}(t^2) = 0$$
利用链式法则和乘积法则,得到
$$x^x(\ln x + 1)\frac{dx}{dt} - x - t\frac{dx}{dt} - 2t = 0$$
解得
$$\frac{dx}{dt} = \frac{x + 2t}{x^x(\ln x + 1) - t}$$
步骤 3:求$\frac{dy}{dt}$
对$\arctan(ty) = \ln(1 + t^2)$关于$t$求导,得到
$$\frac{d}{dt}(\arctan(ty)) = \frac{d}{dt}(\ln(1 + t^2))$$
利用链式法则,得到
$$\frac{1}{1 + (ty)^2}(y + t\frac{dy}{dt}) = \frac{2t}{1 + t^2}$$
解得
$$\frac{dy}{dt} = \frac{2t(1 + t^2) - y(1 + (ty)^2)}{t(1 + (ty)^2)}$$
步骤 4:求$\frac{dy}{dx}$
将$\frac{dx}{dt}$和$\frac{dy}{dt}$代入$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$,得到
$$\frac{dy}{dx} = \frac{\frac{2t(1 + t^2) - y(1 + (ty)^2)}{t(1 + (ty)^2)}}{\frac{x + 2t}{x^x(\ln x + 1) - t}}$$
化简得到
$$\frac{dy}{dx} = \frac{(2t(1 + t^2) - y(1 + (ty)^2))(x^x(\ln x + 1) - t)}{t(1 + (ty)^2)(x + 2t)}$$