已知 f(x)= ,xgt 0 1 ,x=0 arctan dfrac {2)(x)+a xlt 0" data-width="552" data-height="99" data-size="11794" data-format="png" style="max-width:100%">
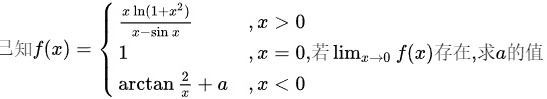
题目解答
答案
首先,我们分析各个分段定义下的 ( f(x) )。
对于 ( x > 0 ):
[
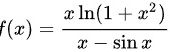
]
当 ( 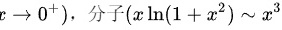 ) 且 分母 (
) 且 分母 (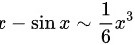 )。代入求极限:
)。代入求极限:
[
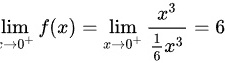
]
计算得到 ( 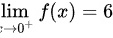 )。
)。
对于 ( x = 0 ):
[
f(0) = 1
]
对于 ( x < 0 ):
[
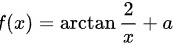
]
当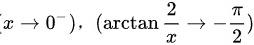 。因此,
。因此,
[
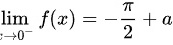
]
为了使 ( 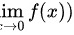 存在,左极限和右极限必须相等:
存在,左极限和右极限必须相等:
[
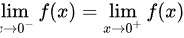
]
由 (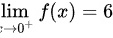 ),得到 (
),得到 ( 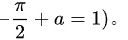
解方程得:
[
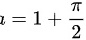
]
解析
考查要点:本题主要考查分段函数在分段点处的极限存在性条件,涉及等价无穷小替换、泰勒展开的应用,以及左右极限相等的判断。
解题核心思路:
- 分别计算$x \to 0^+$和$x \to 0^-$的极限,确保左右极限相等;
- 利用等价无穷小简化计算,如$\ln(1+x^2) \sim x^2$和$x - \sin x \sim \frac{1}{6}x^3$;
- 结合$\arctan$函数的极限性质,处理$x < 0$时的表达式。
破题关键点:
- 右极限:分子分母同阶无穷小的化简;
- 左极限:$\arctan$函数在负无穷处的极限值;
- 等式建立:左右极限相等,解出$a$的值。
当$x \to 0^+$时
函数表达式为:
$f(x) = \frac{x \ln(1+x^2)}{x - \sin x}$
分子化简
当$x \to 0$时,$\ln(1+x^2) \sim x^2$,因此分子:
$x \ln(1+x^2) \sim x \cdot x^2 = x^3$
分母化简
利用泰勒展开$\sin x = x - \frac{x^3}{6} + o(x^3)$,得:
$x - \sin x = x - \left(x - \frac{x^3}{6}\right) = \frac{x^3}{6} + o(x^3) \sim \frac{x^3}{6}$
计算极限
$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} \frac{x^3}{\frac{x^3}{6}} = 6$
当$x \to 0^-$时
函数表达式为:
$f(x) = \arctan\left(\frac{2}{x}\right) + a$
$\arctan$函数的极限
当$x \to 0^-$时,$\frac{2}{x} \to -\infty$,因此:
$\arctan\left(\frac{2}{x}\right) \to -\frac{\pi}{2}$
计算极限
$\lim_{x \to 0^-} f(x) = -\frac{\pi}{2} + a$
极限存在条件
若$\lim_{x \to 0} f(x)$存在,则左右极限相等:
$-\frac{\pi}{2} + a = 6$
解得:
$a = 6 + \frac{\pi}{2}$