题目
当时,与相比是() 高阶无穷小相比 低阶无穷小 等价无穷小 同阶无穷小但不等价无穷小
当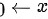 时,
时,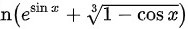 与
与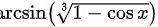 相比是()
相比是()
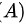 高阶无穷小相比
高阶无穷小相比
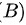 低阶无穷小
低阶无穷小
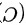 等价无穷小
等价无穷小
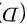 同阶无穷小但不等价无穷小
同阶无穷小但不等价无穷小
题目解答
答案
我们先计算极限:
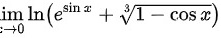
当 趋近于
趋近于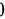 时,
时,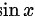 和
和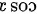 的值都接近
的值都接近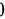 ,所以
,所以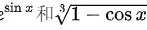 的值都接近
的值都接近 。因此,
。因此,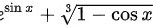 的值接近
的值接近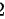 ,所以
,所以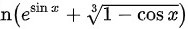 的值接近
的值接近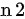 。
。
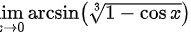
当 趋近于
趋近于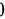 时,
时,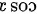 的值接近
的值接近 ,所以
,所以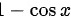 的值接近
的值接近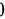 。而
。而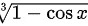 的值接近
的值接近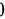 的立方根,即
的立方根,即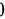 。因此,
。因此,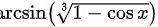 的值接近
的值接近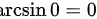 。
。
综上所述,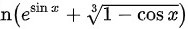 的极限是一个非零常数,而
的极限是一个非零常数,而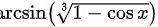 的极限是
的极限是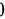 。所以它们不是同阶无穷小,也不是等价无穷小。因为非零常数和
。所以它们不是同阶无穷小,也不是等价无穷小。因为非零常数和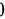 的比较结果是"高阶无穷小相比"(选项
的比较结果是"高阶无穷小相比"(选项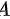 为正确选项)。
为正确选项)。
解析
步骤 1:计算极限 $\lim _{x\rightarrow 0}\ln ({e}^{\sin x}+\sqrt [3]{1-\cos x})$
当 $x$ 趋近于 $0$ 时,$\sin x$ 和 $\cos x$ 的值都接近 $0$,所以 ${e}^{\sin x}$ 和 $\sqrt [3]{1-\cos x}$ 的值都接近 $1$。因此,${e}^{\sin x}+\sqrt [3]{1-\cos x}$ 的值接近 $2$,所以 $n({e}^{\sin x}+\sqrt [3]{1-\cos x})$ 的值接近 $n2$。
步骤 2:计算极限 $\lim _{x\rightarrow 0}\arcsin (\sqrt [3]{1-\cos x})$
当 $x$ 趋近于 $0$ 时,$\cos x$ 的值接近 $1$,所以 $1-\cos x$ 的值接近 $0$。而 $\sqrt [3]{1-\cos x}$ 的值接近 $0$ 的立方根,即 $0$。因此,$r\cos (\sqrt [3]{1-\cos x})$ 的值接近 $r\cos 0=0$。
步骤 3:比较两个极限
综上所述,$n({e}^{\sin x}+\sqrt [3]{1-\cos x})$ 的极限是一个非零常数,而 $r\cos (\sqrt [3]{1-\cos x})$ 的极限是 $0$。所以它们不是同阶无穷小,也不是等价无穷小。因为非零常数和 $0$ 的比较结果是"高阶无穷小相比"(选项为正确选项)。
当 $x$ 趋近于 $0$ 时,$\sin x$ 和 $\cos x$ 的值都接近 $0$,所以 ${e}^{\sin x}$ 和 $\sqrt [3]{1-\cos x}$ 的值都接近 $1$。因此,${e}^{\sin x}+\sqrt [3]{1-\cos x}$ 的值接近 $2$,所以 $n({e}^{\sin x}+\sqrt [3]{1-\cos x})$ 的值接近 $n2$。
步骤 2:计算极限 $\lim _{x\rightarrow 0}\arcsin (\sqrt [3]{1-\cos x})$
当 $x$ 趋近于 $0$ 时,$\cos x$ 的值接近 $1$,所以 $1-\cos x$ 的值接近 $0$。而 $\sqrt [3]{1-\cos x}$ 的值接近 $0$ 的立方根,即 $0$。因此,$r\cos (\sqrt [3]{1-\cos x})$ 的值接近 $r\cos 0=0$。
步骤 3:比较两个极限
综上所述,$n({e}^{\sin x}+\sqrt [3]{1-\cos x})$ 的极限是一个非零常数,而 $r\cos (\sqrt [3]{1-\cos x})$ 的极限是 $0$。所以它们不是同阶无穷小,也不是等价无穷小。因为非零常数和 $0$ 的比较结果是"高阶无穷小相比"(选项为正确选项)。