题目
8 ) =ln (x+sqrt ({a)^2+(x)^2}) );
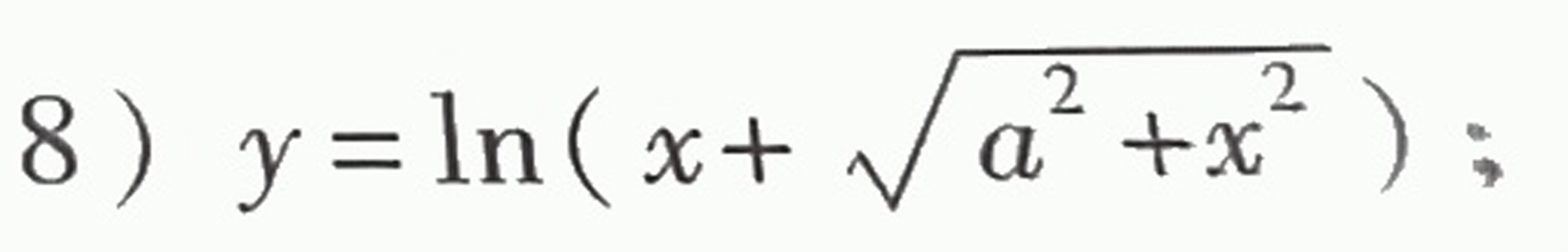
题目解答
答案
式的求导,根据对数函数的求导公式,复合函数求导公式,即可求。
$y=\ln (x+\sqrt {{a}^{2}+{x}^{2}})$
$y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot (1+\frac{2x}{2\sqrt {{a}^{2}+{x}^{2}}})$
$=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot \frac{\sqrt {{a}^{2}+{x}^{2}}+x}{\sqrt {{a}^{2}+{x}^{2}}}$
$=\frac{1}{\sqrt {{a}^{2}+{x}^{2}}}$
$=\frac{\sqrt {{a}^{2}+{x}^{2}}}{{a}^{2}+{x}^{2}}$
$y=\ln (x+\sqrt {{a}^{2}+{x}^{2}})$
$y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot (1+\frac{2x}{2\sqrt {{a}^{2}+{x}^{2}}})$
$=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot \frac{\sqrt {{a}^{2}+{x}^{2}}+x}{\sqrt {{a}^{2}+{x}^{2}}}$
$=\frac{1}{\sqrt {{a}^{2}+{x}^{2}}}$
$=\frac{\sqrt {{a}^{2}+{x}^{2}}}{{a}^{2}+{x}^{2}}$
解析
步骤 1:复合函数求导
根据复合函数求导法则,$y=\ln (x+\sqrt {{a}^{2}+{x}^{2}})$ 的导数为 $y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot (x+\sqrt {{a}^{2}+{x}^{2}})'$。
步骤 2:求导内部函数
$(x+\sqrt {{a}^{2}+{x}^{2}})'=1+\frac{1}{2}\cdot (2x)\cdot ({a}^{2}+{x}^{2})^{-\frac{1}{2}}=1+\frac{x}{\sqrt {{a}^{2}+{x}^{2}}}$。
步骤 3:简化表达式
将步骤 2 的结果代入步骤 1 的表达式中,得到 $y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot (1+\frac{x}{\sqrt {{a}^{2}+{x}^{2}}})$。
步骤 4:进一步简化
$y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot \frac{\sqrt {{a}^{2}+{x}^{2}}+x}{\sqrt {{a}^{2}+{x}^{2}}}=\frac{1}{\sqrt {{a}^{2}+{x}^{2}}}$。
根据复合函数求导法则,$y=\ln (x+\sqrt {{a}^{2}+{x}^{2}})$ 的导数为 $y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot (x+\sqrt {{a}^{2}+{x}^{2}})'$。
步骤 2:求导内部函数
$(x+\sqrt {{a}^{2}+{x}^{2}})'=1+\frac{1}{2}\cdot (2x)\cdot ({a}^{2}+{x}^{2})^{-\frac{1}{2}}=1+\frac{x}{\sqrt {{a}^{2}+{x}^{2}}}$。
步骤 3:简化表达式
将步骤 2 的结果代入步骤 1 的表达式中,得到 $y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot (1+\frac{x}{\sqrt {{a}^{2}+{x}^{2}}})$。
步骤 4:进一步简化
$y'=\frac{1}{x+\sqrt {{a}^{2}+{x}^{2}}}\cdot \frac{\sqrt {{a}^{2}+{x}^{2}}+x}{\sqrt {{a}^{2}+{x}^{2}}}=\frac{1}{\sqrt {{a}^{2}+{x}^{2}}}$。