题目
求微分方程 (2x+y-4)dx+(x+y-1)dy=0 的通解.
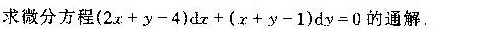
题目解答
答案

解析
步骤 1:将原方程转换为齐次方程
原方程为 $(2x+y-4)dx+(x+y-1)dy=0$。为了将其转换为齐次方程,我们引入新的变量 $X=x+h$ 和 $Y=y+k$,其中 $h$ 和 $k$ 是待定常数。这样,原方程可以写为 $(2X+Y+2h+k-4)dX+(X+Y+h+k-1)dY=0$。为了使方程成为齐次方程,我们需要选择 $h$ 和 $k$ 使得 $2h+k-4=0$ 和 $h+k-1=0$。解这个方程组,我们得到 $h=3$ 和 $k=-2$。因此,我们令 $x=X-3$ 和 $y=Y-2$,代入原方程,得到 $(2X+Y)dx+(X+Y)dY=0$。
步骤 2:求解齐次方程
将方程 $(2X+Y)dx+(X+Y)dY=0$ 重写为 $\dfrac{dY}{dX}=-\dfrac{2X+Y}{X+Y}$。这是一个齐次方程,我们可以通过令 $Y=UX$ 来求解,其中 $U=\dfrac{Y}{X}$。因此,$dY=UdX+XdU$。将 $Y=UX$ 和 $dY=UdX+XdU$ 代入方程,得到 $UdX+XdU=-\dfrac{2X+UX}{X+UX}dX$。化简后得到 $XdU=-\dfrac{2+U}{1+U}dX$。分离变量,得到 $\dfrac{1+U}{2+2U+U^2}dU=-\dfrac{dX}{X}$。积分得到 $\ln|C_1|+\dfrac{1}{2}\ln|U^2+2U+2|=\ln|X|$,即 $C_1\sqrt{U^2+2U+2}=X$。代回 $U=\dfrac{Y}{X}$,得到 $C_1\sqrt{\dfrac{Y^2}{X^2}+\dfrac{2Y}{X}+2}=X$,即 $C_1\sqrt{Y^2+2XY+2X^2}=X^2$。化简得到 $Y^2+2XY+2X^2=C_2X^2$,其中 $C_2=C_1^2$。
步骤 3:代回原变量
将 $X=x+3$ 和 $Y=y+2$ 代入上式,得到 $(y+2)^2+2(x+3)(y+2)+2(x+3)^2=C_2(x+3)^2$。化简得到 $2x^2+2xy+y^2-8x-2y=C$,其中 $C=C_2-10$。
原方程为 $(2x+y-4)dx+(x+y-1)dy=0$。为了将其转换为齐次方程,我们引入新的变量 $X=x+h$ 和 $Y=y+k$,其中 $h$ 和 $k$ 是待定常数。这样,原方程可以写为 $(2X+Y+2h+k-4)dX+(X+Y+h+k-1)dY=0$。为了使方程成为齐次方程,我们需要选择 $h$ 和 $k$ 使得 $2h+k-4=0$ 和 $h+k-1=0$。解这个方程组,我们得到 $h=3$ 和 $k=-2$。因此,我们令 $x=X-3$ 和 $y=Y-2$,代入原方程,得到 $(2X+Y)dx+(X+Y)dY=0$。
步骤 2:求解齐次方程
将方程 $(2X+Y)dx+(X+Y)dY=0$ 重写为 $\dfrac{dY}{dX}=-\dfrac{2X+Y}{X+Y}$。这是一个齐次方程,我们可以通过令 $Y=UX$ 来求解,其中 $U=\dfrac{Y}{X}$。因此,$dY=UdX+XdU$。将 $Y=UX$ 和 $dY=UdX+XdU$ 代入方程,得到 $UdX+XdU=-\dfrac{2X+UX}{X+UX}dX$。化简后得到 $XdU=-\dfrac{2+U}{1+U}dX$。分离变量,得到 $\dfrac{1+U}{2+2U+U^2}dU=-\dfrac{dX}{X}$。积分得到 $\ln|C_1|+\dfrac{1}{2}\ln|U^2+2U+2|=\ln|X|$,即 $C_1\sqrt{U^2+2U+2}=X$。代回 $U=\dfrac{Y}{X}$,得到 $C_1\sqrt{\dfrac{Y^2}{X^2}+\dfrac{2Y}{X}+2}=X$,即 $C_1\sqrt{Y^2+2XY+2X^2}=X^2$。化简得到 $Y^2+2XY+2X^2=C_2X^2$,其中 $C_2=C_1^2$。
步骤 3:代回原变量
将 $X=x+3$ 和 $Y=y+2$ 代入上式,得到 $(y+2)^2+2(x+3)(y+2)+2(x+3)^2=C_2(x+3)^2$。化简得到 $2x^2+2xy+y^2-8x-2y=C$,其中 $C=C_2-10$。