题目
(1)lim _(xarrow 3)dfrac (sqrt {{x)^3+9}-6}(2-sqrt {{x)^3-23}}=-|||-__-|||-__ _.(2)设lim _(xarrow 3)dfrac (sqrt {{x)^3+9}-6}(2-sqrt {{x)^3-23}}=-|||-__-|||-__，且lim _(xarrow 3)dfrac (sqrt {{x)^3+9}-6}(2-sqrt {{x)^3-23}}=-|||-__-|||-__有连续的二阶偏导数，则lim _(xarrow 3)dfrac (sqrt {{x)^3+9}-6}(2-sqrt {{x)^3-23}}=-|||-__-|||-__ _.
(1)
_.
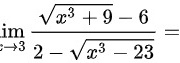(2)设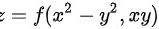
，且
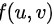有连续的二阶偏导数，则
_.
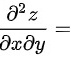题目解答
答案
解：(1)原式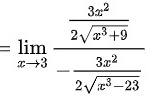
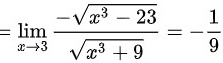
(2)首先引进符号：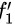
表示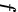
对第一个中间变量的偏导数，
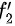表示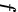对第二个中间变量的偏导数，则
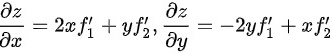
这里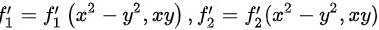
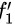，即与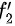仍是复合函数，再引进符号：用
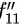表示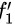后再对第一个中间变量的偏导数，
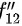表示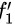再对第二个中间变量的偏导数；类似地定义
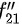和
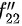，从而
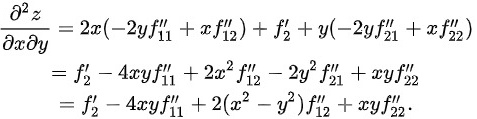
故答案为：(1)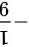
；
(2)
.
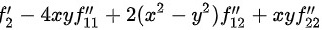解析
(1) 步骤 1：分子分母同时乘以各自的共轭表达式
原式$=\lim _{x\rightarrow 3}\dfrac {(\sqrt {{x}^{3}+9}-6)(\sqrt {{x}^{3}+9}+6)(2+\sqrt {{x}^{3}-23})}{(2-\sqrt {{x}^{3}-23})(2+\sqrt {{x}^{3}-23})(\sqrt {{x}^{3}+9}+6)}$
步骤 2：化简表达式
$=\lim _{x\rightarrow 3}\dfrac {({x}^{3}+9-36)(2+\sqrt {{x}^{3}-23})}{(4-({x}^{3}-23))(\sqrt {{x}^{3}+9}+6)}$
步骤 3：进一步化简
$=\lim _{x\rightarrow 3}\dfrac {({x}^{3}-27)(2+\sqrt {{x}^{3}-23})}{(27-{x}^{3})(\sqrt {{x}^{3}+9}+6)}$
步骤 4：提取公因式并计算极限
$=\lim _{x\rightarrow 3}\dfrac {-(2+\sqrt {{x}^{3}-23})}{(\sqrt {{x}^{3}+9}+6)}=-\dfrac {1}{9}$
(2) 步骤 1：计算一阶偏导数
$\dfrac {\partial z}{\partial x}=2x{f}_{1}'+y{f}_{2}'$ ,$\dfrac {\partial z}{\partial y}=-2y{f}_{1}+x{f}_{2}$
步骤 2：计算二阶偏导数
$\dfrac {{\partial }^{2}z}{\partial x\partial y}=\dfrac {\partial }{\partial y}(2x{f}_{1}'+y{f}_{2}')$
$=2x\dfrac {\partial {f}_{1}'}{\partial y}+{f}_{2}'+y\dfrac {\partial {f}_{2}'}{\partial y}$
$=2x({f}_{11}^{11}(-2y)+{f}_{12}^{11}x)+{f}_{2}'+y({f}_{21}^{11}(-2y)+{f}_{22}^{11}x)$
$={f}_{2}'+2x{f}_{12}^{11}x-4xy{f}_{11}^{11}+xy{f}_{22}^{11}-2{y}^{2}{f}_{21}^{11}$
$={f}_{2}'+2({x}^{2}-{y}^{2}){f}_{12}^{11}-4xy{f}_{11}^{11}+xy{f}_{22}^{11}$
原式$=\lim _{x\rightarrow 3}\dfrac {(\sqrt {{x}^{3}+9}-6)(\sqrt {{x}^{3}+9}+6)(2+\sqrt {{x}^{3}-23})}{(2-\sqrt {{x}^{3}-23})(2+\sqrt {{x}^{3}-23})(\sqrt {{x}^{3}+9}+6)}$
步骤 2：化简表达式
$=\lim _{x\rightarrow 3}\dfrac {({x}^{3}+9-36)(2+\sqrt {{x}^{3}-23})}{(4-({x}^{3}-23))(\sqrt {{x}^{3}+9}+6)}$
步骤 3：进一步化简
$=\lim _{x\rightarrow 3}\dfrac {({x}^{3}-27)(2+\sqrt {{x}^{3}-23})}{(27-{x}^{3})(\sqrt {{x}^{3}+9}+6)}$
步骤 4：提取公因式并计算极限
$=\lim _{x\rightarrow 3}\dfrac {-(2+\sqrt {{x}^{3}-23})}{(\sqrt {{x}^{3}+9}+6)}=-\dfrac {1}{9}$
(2) 步骤 1：计算一阶偏导数
$\dfrac {\partial z}{\partial x}=2x{f}_{1}'+y{f}_{2}'$ ,$\dfrac {\partial z}{\partial y}=-2y{f}_{1}+x{f}_{2}$
步骤 2：计算二阶偏导数
$\dfrac {{\partial }^{2}z}{\partial x\partial y}=\dfrac {\partial }{\partial y}(2x{f}_{1}'+y{f}_{2}')$
$=2x\dfrac {\partial {f}_{1}'}{\partial y}+{f}_{2}'+y\dfrac {\partial {f}_{2}'}{\partial y}$
$=2x({f}_{11}^{11}(-2y)+{f}_{12}^{11}x)+{f}_{2}'+y({f}_{21}^{11}(-2y)+{f}_{22}^{11}x)$
$={f}_{2}'+2x{f}_{12}^{11}x-4xy{f}_{11}^{11}+xy{f}_{22}^{11}-2{y}^{2}{f}_{21}^{11}$
$={f}_{2}'+2({x}^{2}-{y}^{2}){f}_{12}^{11}-4xy{f}_{11}^{11}+xy{f}_{22}^{11}$