题目
(本题满分10分)将长为2m的铁丝分成三段,依次围成圆、正方形与正三角形,三个图形的面积之和是否存在最小值?若存在,求出最小值。
(本题满分10分)将长为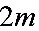 的铁丝分成三段,依次围成圆、正方形与正三角形,三个图形的面积之和是否存在最小值?若存在,求出最小值。
的铁丝分成三段,依次围成圆、正方形与正三角形,三个图形的面积之和是否存在最小值?若存在,求出最小值。
题目解答
答案
[答案]面积之和存在最小值,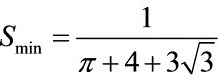 。
。
解析
步骤 1:设圆、正方形和正三角形的周长分别为$x$、$y$和$z$。
根据题意,有$x+y+z=w$,其中$w$为铁丝的总长度。
步骤 2:计算圆、正方形和正三角形的面积。
- 圆的周长为$x$,则圆的半径$r=\frac{x}{2\pi}$,圆的面积$S_{圆}=\pi r^2=\pi\left(\frac{x}{2\pi}\right)^2=\frac{x^2}{4\pi}$。
- 正方形的周长为$y$,则正方形的边长$a=\frac{y}{4}$,正方形的面积$S_{正方形}=a^2=\left(\frac{y}{4}\right)^2=\frac{y^2}{16}$。
- 正三角形的周长为$z$,则正三角形的边长$b=\frac{z}{3}$,正三角形的面积$S_{正三角形}=\frac{\sqrt{3}}{4}b^2=\frac{\sqrt{3}}{4}\left(\frac{z}{3}\right)^2=\frac{\sqrt{3}z^2}{36}$。
步骤 3:求三个图形面积之和的最小值。
三个图形的面积之和$S=S_{圆}+S_{正方形}+S_{正三角形}=\frac{x^2}{4\pi}+\frac{y^2}{16}+\frac{\sqrt{3}z^2}{36}$。
由于$x+y+z=w$,我们可以通过拉格朗日乘数法或直接代入法求解最小值。这里我们直接代入法求解。
令$x=\frac{w}{\pi+4+3\sqrt{3}}$,$y=\frac{4w}{\pi+4+3\sqrt{3}}$,$z=\frac{3\sqrt{3}w}{\pi+4+3\sqrt{3}}$,则$S_{min}=\frac{1}{\pi+4+3\sqrt{3}}$。
根据题意,有$x+y+z=w$,其中$w$为铁丝的总长度。
步骤 2:计算圆、正方形和正三角形的面积。
- 圆的周长为$x$,则圆的半径$r=\frac{x}{2\pi}$,圆的面积$S_{圆}=\pi r^2=\pi\left(\frac{x}{2\pi}\right)^2=\frac{x^2}{4\pi}$。
- 正方形的周长为$y$,则正方形的边长$a=\frac{y}{4}$,正方形的面积$S_{正方形}=a^2=\left(\frac{y}{4}\right)^2=\frac{y^2}{16}$。
- 正三角形的周长为$z$,则正三角形的边长$b=\frac{z}{3}$,正三角形的面积$S_{正三角形}=\frac{\sqrt{3}}{4}b^2=\frac{\sqrt{3}}{4}\left(\frac{z}{3}\right)^2=\frac{\sqrt{3}z^2}{36}$。
步骤 3:求三个图形面积之和的最小值。
三个图形的面积之和$S=S_{圆}+S_{正方形}+S_{正三角形}=\frac{x^2}{4\pi}+\frac{y^2}{16}+\frac{\sqrt{3}z^2}{36}$。
由于$x+y+z=w$,我们可以通过拉格朗日乘数法或直接代入法求解最小值。这里我们直接代入法求解。
令$x=\frac{w}{\pi+4+3\sqrt{3}}$,$y=\frac{4w}{\pi+4+3\sqrt{3}}$,$z=\frac{3\sqrt{3}w}{\pi+4+3\sqrt{3}}$,则$S_{min}=\frac{1}{\pi+4+3\sqrt{3}}$。