题目
求极限lim _(narrow infty )(dfrac (1)({n)^2+n+1}+dfrac (2)({n)^2+n+2}+... +dfrac (n)({n)^2+n+n})=_____.
求极限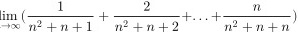 =_____.
=_____.
题目解答
答案
当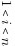 时,有
时,有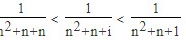 ,
,
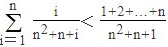
又:
故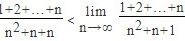
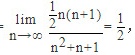
由夹逼准则有: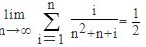 .
.
解析
步骤 1:确定每一项的范围
对于每一项$\dfrac{i}{{n}^{2}+n+i}$,其中$i$从$1$到$n$,我们有:
$$\dfrac{i}{{n}^{2}+n+n} \leq \dfrac{i}{{n}^{2}+n+i} \leq \dfrac{i}{{n}^{2}+n+1}$$
步骤 2:求和
将上述不等式对$i$从$1$到$n$求和,得到:
$$\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+n} \leq \sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+i} \leq \sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+1}$$
步骤 3:计算求和的极限
计算求和的极限,我们有:
$$\lim_{n\to\infty}\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+n} = \lim_{n\to\infty}\dfrac{\dfrac{1}{2}n(n+1)}{{n}^{2}+n+n} = \dfrac{1}{2}$$
$$\lim_{n\to\infty}\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+1} = \lim_{n\to\infty}\dfrac{\dfrac{1}{2}n(n+1)}{{n}^{2}+n+1} = \dfrac{1}{2}$$
步骤 4:应用夹逼准则
根据夹逼准则,我们得到:
$$\lim_{n\to\infty}\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+i} = \dfrac{1}{2}$$
对于每一项$\dfrac{i}{{n}^{2}+n+i}$,其中$i$从$1$到$n$,我们有:
$$\dfrac{i}{{n}^{2}+n+n} \leq \dfrac{i}{{n}^{2}+n+i} \leq \dfrac{i}{{n}^{2}+n+1}$$
步骤 2:求和
将上述不等式对$i$从$1$到$n$求和,得到:
$$\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+n} \leq \sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+i} \leq \sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+1}$$
步骤 3:计算求和的极限
计算求和的极限,我们有:
$$\lim_{n\to\infty}\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+n} = \lim_{n\to\infty}\dfrac{\dfrac{1}{2}n(n+1)}{{n}^{2}+n+n} = \dfrac{1}{2}$$
$$\lim_{n\to\infty}\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+1} = \lim_{n\to\infty}\dfrac{\dfrac{1}{2}n(n+1)}{{n}^{2}+n+1} = \dfrac{1}{2}$$
步骤 4:应用夹逼准则
根据夹逼准则,我们得到:
$$\lim_{n\to\infty}\sum_{i=1}^{n}\dfrac{i}{{n}^{2}+n+i} = \dfrac{1}{2}$$