题目
下列矩阵中不能相似对角化的矩阵一共有( )。2 -1 2 1 0 0-|||-1 11 1 1-|||-5 -3 3 1 2 2-|||-L 2 2 -1 -1-|||--1 0 -2 1 1 3 ( A ) 1 个. ( B ) 2 个 . ( C ) 3 个 . ( D ) 0 个
下列矩阵中不能相似对角化的矩阵一共有( )。
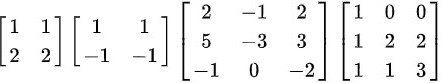
( A ) 1 个. ( B ) 2 个 . ( C ) 3 个 . ( D ) 0 个
题目解答
答案
根据题意,此题考查的是线性代数中的相似对角化,
首先.第一个是有2个不同的特征值,不可对角化
第二个是有2个不同的特征值,不可对角化
第三个有相同的特征值,不可对角化
第四个有3个不同的特征值,可对角化
能相似对角化的矩阵只有一个,故选 A
解析
步骤 1:确定矩阵的特征值
对于每个矩阵,我们首先需要计算其特征值。特征值是通过求解矩阵的特征方程 \(\det(A - \lambda I) = 0\) 得到的,其中 \(A\) 是给定的矩阵,\(I\) 是单位矩阵,\(\lambda\) 是特征值。
步骤 2:判断特征值的重数
如果一个矩阵有 \(n\) 个不同的特征值,那么它一定可以相似对角化。如果一个矩阵有重复的特征值,我们需要进一步检查每个特征值对应的特征向量的个数。如果每个特征值的代数重数(即特征值的重复次数)等于其几何重数(即对应特征值的线性无关特征向量的个数),那么矩阵可以相似对角化。否则,矩阵不能相似对角化。
步骤 3:计算每个矩阵的特征值和特征向量
对于每个矩阵,计算其特征值和特征向量,然后根据步骤 2 的规则判断矩阵是否可以相似对角化。
步骤 4:统计不能相似对角化的矩阵数量
根据步骤 3 的结果,统计不能相似对角化的矩阵数量。
对于每个矩阵,我们首先需要计算其特征值。特征值是通过求解矩阵的特征方程 \(\det(A - \lambda I) = 0\) 得到的,其中 \(A\) 是给定的矩阵,\(I\) 是单位矩阵,\(\lambda\) 是特征值。
步骤 2:判断特征值的重数
如果一个矩阵有 \(n\) 个不同的特征值,那么它一定可以相似对角化。如果一个矩阵有重复的特征值,我们需要进一步检查每个特征值对应的特征向量的个数。如果每个特征值的代数重数(即特征值的重复次数)等于其几何重数(即对应特征值的线性无关特征向量的个数),那么矩阵可以相似对角化。否则,矩阵不能相似对角化。
步骤 3:计算每个矩阵的特征值和特征向量
对于每个矩阵,计算其特征值和特征向量,然后根据步骤 2 的规则判断矩阵是否可以相似对角化。
步骤 4:统计不能相似对角化的矩阵数量
根据步骤 3 的结果,统计不能相似对角化的矩阵数量。