题目
七、(证明题,须写出关键步骤,本题共8分)证明:如果向量组(alpha )_(1),(alpha )_(2),(alpha )_(3)线性无关,则向量组(alpha )_(1),(alpha )_(2),(alpha )_(3)也线性无关。
七、(证明题,须写出关键步骤,本题共8分)证明:如果向量组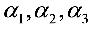
线性无关,则向量组
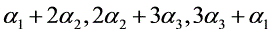也线性无关。
题目解答
答案
证明:设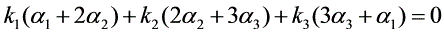
,则
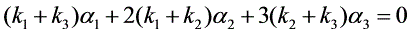
因为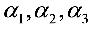线性无关,所以
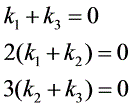……………………………(4分)
解这个方程组,得
所以向量组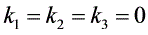
也线性无关。……………(8分)
解析
步骤 1：假设线性组合为零
假设存在一组数${k}_{1},{k}_{2},{k}_{3}$，使得${k}_{1}({\alpha }_{1}+2{\alpha }_{2})+{k}_{2}(2{\alpha }_{2}+3{\alpha }_{3})+{k}_{3}(3{\alpha }_{3}+{\alpha }_{1})=0$。这表示向量组${\alpha }_{1}+2{\alpha }_{2},2{\alpha }_{2}+3{\alpha }_{3},3{\alpha }_{3}+{\alpha }_{1}$的线性组合为零向量。
步骤 2：展开并整理
将上述表达式展开，得到$({k}_{1}+{k}_{3}){\alpha }_{1}+2({k}_{1}+{k}_{2}){\alpha }_{2}+3({k}_{2}+{k}_{3}){\alpha }_{3}=0$。由于${\alpha }_{1},{\alpha }_{2},{\alpha }_{3}$线性无关，这意味着它们的系数必须全部为零。
步骤 3：解方程组
根据线性无关的定义，我们得到方程组：
${k}_{1}+{k}_{3}=0$
$2({k}_{1}+{k}_{2})=0$
$3({k}_{2}+{k}_{3})=0$
解这个方程组，得到${k}_{1}={k}_{2}={k}_{3}=0$。这意味着只有当${k}_{1},{k}_{2},{k}_{3}$都为零时，上述线性组合才为零向量。
假设存在一组数${k}_{1},{k}_{2},{k}_{3}$，使得${k}_{1}({\alpha }_{1}+2{\alpha }_{2})+{k}_{2}(2{\alpha }_{2}+3{\alpha }_{3})+{k}_{3}(3{\alpha }_{3}+{\alpha }_{1})=0$。这表示向量组${\alpha }_{1}+2{\alpha }_{2},2{\alpha }_{2}+3{\alpha }_{3},3{\alpha }_{3}+{\alpha }_{1}$的线性组合为零向量。
步骤 2：展开并整理
将上述表达式展开，得到$({k}_{1}+{k}_{3}){\alpha }_{1}+2({k}_{1}+{k}_{2}){\alpha }_{2}+3({k}_{2}+{k}_{3}){\alpha }_{3}=0$。由于${\alpha }_{1},{\alpha }_{2},{\alpha }_{3}$线性无关，这意味着它们的系数必须全部为零。
步骤 3：解方程组
根据线性无关的定义，我们得到方程组：
${k}_{1}+{k}_{3}=0$
$2({k}_{1}+{k}_{2})=0$
$3({k}_{2}+{k}_{3})=0$
解这个方程组，得到${k}_{1}={k}_{2}={k}_{3}=0$。这意味着只有当${k}_{1},{k}_{2},{k}_{3}$都为零时，上述线性组合才为零向量。