题目
lim _(xarrow 0)dfrac (1)(x)sin dfrac (1)(x)？
？
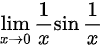题目解答
答案
解：由题可知，当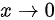
时，
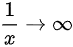，而函数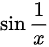
是一个有界函数，因此该极限变为无穷大乘以一个有界函数，
∴极限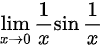不存在但不为
。
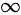解析
步骤 1：分析函数行为
当$x\rightarrow 0$时，$\dfrac {1}{x}\rightarrow \infty $，而$\sin \dfrac {1}{x}$是一个有界函数，其值域为$[-1,1]$。这意味着$\sin \dfrac {1}{x}$的值在$-1$和$1$之间波动，但不会超过这个范围。
步骤 2：考虑极限的定义
极限$\lim _{x\rightarrow 0}\dfrac {1}{x}\sin \dfrac {1}{x}$表示当$x$无限接近于$0$时，函数$\dfrac {1}{x}\sin \dfrac {1}{x}$的值趋向于某个确定的值。然而，由于$\sin \dfrac {1}{x}$在$x\rightarrow 0$时的振荡特性，$\dfrac {1}{x}\sin \dfrac {1}{x}$的值会随着$x$的减小而无限增大或减小，但不会收敛到一个特定的值。
步骤 3：确定极限不存在
由于$\sin \dfrac {1}{x}$的振荡特性，$\dfrac {1}{x}\sin \dfrac {1}{x}$的值在$x\rightarrow 0$时不会收敛到一个特定的值，因此该极限不存在。但是，由于$\dfrac {1}{x}$的值趋向于无穷大，极限不为无穷大，而是不存在。
当$x\rightarrow 0$时，$\dfrac {1}{x}\rightarrow \infty $，而$\sin \dfrac {1}{x}$是一个有界函数，其值域为$[-1,1]$。这意味着$\sin \dfrac {1}{x}$的值在$-1$和$1$之间波动，但不会超过这个范围。
步骤 2：考虑极限的定义
极限$\lim _{x\rightarrow 0}\dfrac {1}{x}\sin \dfrac {1}{x}$表示当$x$无限接近于$0$时，函数$\dfrac {1}{x}\sin \dfrac {1}{x}$的值趋向于某个确定的值。然而，由于$\sin \dfrac {1}{x}$在$x\rightarrow 0$时的振荡特性，$\dfrac {1}{x}\sin \dfrac {1}{x}$的值会随着$x$的减小而无限增大或减小，但不会收敛到一个特定的值。
步骤 3：确定极限不存在
由于$\sin \dfrac {1}{x}$的振荡特性，$\dfrac {1}{x}\sin \dfrac {1}{x}$的值在$x\rightarrow 0$时不会收敛到一个特定的值，因此该极限不存在。但是，由于$\dfrac {1}{x}$的值趋向于无穷大，极限不为无穷大，而是不存在。