(3)lim _(xarrow 1)dfrac (ln (2-x)arctan x)(sin ({x)^2-1)}
(3)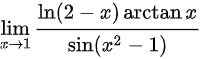
题目解答
答案
解:
(3)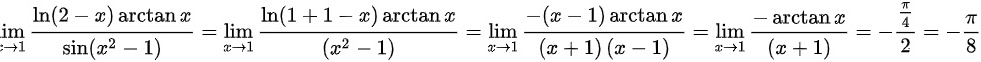
解析
考查要点:本题主要考查极限的计算,特别是等价无穷小替换和洛必达法则的应用,以及对复合函数在特定点附近展开的理解。
解题核心思路:
当$x \rightarrow 1$时,分子$\ln(2-x)\arctan x$和分母$\sin(x^2-1)$均趋近于$0$,形成$\frac{0}{0}$型不定式。此时可选择等价无穷小替换或洛必达法则简化计算。关键在于将分子和分母中的函数展开为低阶项,或通过求导消去零因子。
破题关键点:
- 变量替换:令$t = x - 1$,将$x \rightarrow 1$转化为$t \rightarrow 0$,简化表达式。
- 等价无穷小替换:利用$\ln(1-t) \approx -t$和$\sin(2t) \approx 2t$,快速化简分子和分母。
- 洛必达法则:对分子和分母分别求导,直接计算极限。
步骤1:变量替换
令$t = x - 1$,当$x \rightarrow 1$时,$t \rightarrow 0$。原式变形为:
$\lim_{t \rightarrow 0} \frac{\ln(1 - t) \cdot \arctan(1 + t)}{\sin(2t + t^2)}$
步骤2:等价无穷小替换
- $\ln(1 - t) \approx -t$(当$t \rightarrow 0$时)
- $\sin(2t + t^2) \approx 2t$(当$t \rightarrow 0$时,$t^2$可忽略)
- $\arctan(1 + t) \approx \frac{\pi}{4} + \frac{t}{2}$(泰勒展开一阶近似)
步骤3:代入近似式化简
分子:
$\ln(1 - t) \cdot \arctan(1 + t) \approx (-t) \cdot \left(\frac{\pi}{4} + \frac{t}{2}\right) = -\frac{\pi t}{4} - \frac{t^2}{2}$
分母:
$\sin(2t + t^2) \approx 2t$
因此,原式化简为:
$\lim_{t \rightarrow 0} \frac{-\frac{\pi t}{4} - \frac{t^2}{2}}{2t} = \lim_{t \rightarrow 0} \left( -\frac{\pi}{8} - \frac{t}{4} \right) = -\frac{\pi}{8}$
步骤4(备选):洛必达法则验证
对分子和分母分别求导:
- 分子导数:
$\frac{d}{dx} \left[ \ln(2 - x) \cdot \arctan x \right] = -\frac{\arctan x}{2 - x} + \frac{\ln(2 - x)}{1 + x^2}$
代入$x = 1$得:
$-\frac{\pi/4}{1} + \frac{0}{2} = -\frac{\pi}{4}$ - 分母导数:
$\frac{d}{dx} \left[ \sin(x^2 - 1) \right] = 2x \cos(x^2 - 1)$
代入$x = 1$得:
$2 \cdot 1 \cdot \cos(0) = 2$
因此,极限值为:
$\frac{-\pi/4}{2} = -\frac{\pi}{8}$