题目
(本题满分11分)已知向量组I: (alpha )_(1)=((1,1,4))^T, (alpha )_(2)=((1,0,4))^T, _(3)=((1,2,{a)^2+3)}^rI: (alpha )_(1)=((1,1,4))^T, (alpha )_(2)=((1,0,4))^T, _(3)=((1,2,{a)^2+3)}^r若向量组Ⅰ与向量组Ⅱ等价,求a的取值,并将β3用α1, α2, α3线性表示。
(本题满分11分)
已知向量组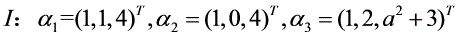
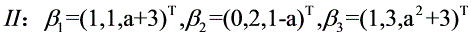
若向量组Ⅰ与向量组Ⅱ等价,求a的取值,并将β3用α1, α2, α3线性表示。
题目解答
答案
[解析]α1, α2, α3与β1, β2, β3等价,则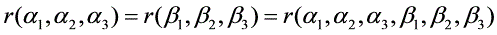
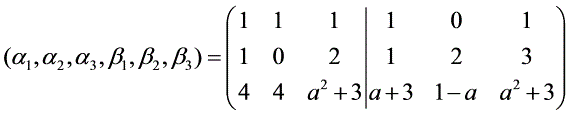

(1)a≠1,则(Ⅰ)与(Ⅱ)等价
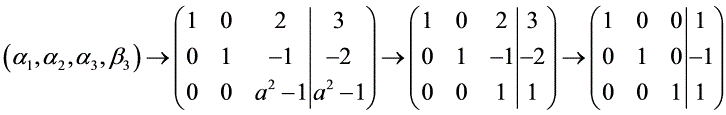
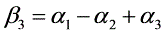
(2)a=1
α1, α2, α3与β1, β2, β3等价
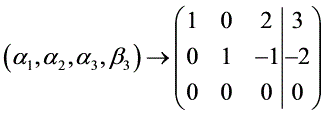
则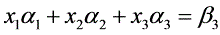 的通解为
的通解为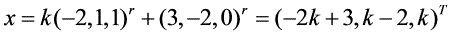
即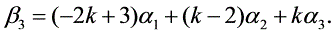
解析
步骤 1:确定向量组I和II的秩
向量组I和II等价,意味着它们的秩相等,且它们的秩等于它们合并后的向量组的秩。因此,我们需要计算向量组I和II的秩,以及它们合并后的向量组的秩。
步骤 2:计算合并后的向量组的秩
将向量组I和II合并,得到矩阵$({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\beta }_{1},{\beta }_{2},{\beta }_{3})$,并进行初等行变换,以确定其秩。
步骤 3:确定a的取值
根据合并后的向量组的秩,确定a的取值,使得向量组I和II的秩相等。
步骤 4:将β3用α1, α2, α3线性表示
根据a的取值,将β3用α1, α2, α3线性表示。
向量组I和II等价,意味着它们的秩相等,且它们的秩等于它们合并后的向量组的秩。因此,我们需要计算向量组I和II的秩,以及它们合并后的向量组的秩。
步骤 2:计算合并后的向量组的秩
将向量组I和II合并,得到矩阵$({\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\beta }_{1},{\beta }_{2},{\beta }_{3})$,并进行初等行变换,以确定其秩。
步骤 3:确定a的取值
根据合并后的向量组的秩,确定a的取值,使得向量组I和II的秩相等。
步骤 4:将β3用α1, α2, α3线性表示
根据a的取值,将β3用α1, α2, α3线性表示。