题目
12.求下列函数的极限.-|||-(7) lim _(xarrow infty )((dfrac {x+3)(x-1))}^x+1;

题目解答
答案
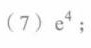
解析
考查要点:本题主要考查无穷大极限的计算,特别是涉及底数趋近于1、指数趋向于无穷大的复合函数极限。需要灵活运用自然对数的极限形式和等价无穷小替换。
解题核心思路:
- 将底数$\dfrac{x+3}{x-1}$变形为$1+\dfrac{4}{x-1}$,使其符合$\left(1+\dfrac{a}{x}\right)^x$的结构;
- 通过变量替换或直接展开对数,将原式转化为与$e^a$相关的形式;
- 利用极限运算性质化简,最终得到结果。
破题关键点:
- 识别底数趋近于1的结构,并将其改写为$1+\dfrac{a}{x}$的形式;
- 正确处理指数中的$x+1$与分母中的$x-1$的关系,通过变量替换或展开对数简化表达式。
步骤1:化简底数
将$\dfrac{x+3}{x-1}$变形为:
$\dfrac{x+3}{x-1} = 1 + \dfrac{4}{x-1}.$
步骤2:变量替换
令$t = x-1$,当$x \to \infty$时,$t \to \infty$。此时原式变为:
$\left(1 + \dfrac{4}{t}\right)^{t + 2}.$
步骤3:拆分表达式
将指数拆分为$t$和$2$两部分:
$\left(1 + \dfrac{4}{t}\right)^t \cdot \left(1 + \dfrac{4}{t}\right)^2.$
步骤4:计算各部分极限
- $\left(1 + \dfrac{4}{t}\right)^t \to e^4$(根据极限公式$\lim_{t \to \infty} \left(1 + \dfrac{a}{t}\right)^t = e^a$);
- $\left(1 + \dfrac{4}{t}\right)^2 \to 1$(因$\dfrac{4}{t} \to 0$)。
步骤5:综合结果
两部分相乘得:
$e^4 \cdot 1 = e^4.$