题目
解答题-|||-函数 f(x)= { , xgt 0 a-1, x=0 .-|||-(1)当a,b为何值时,f(x)在 x=0 处存在极限?-|||-(2)当a,b为何值时,f(x)在 x=0 处连续?

题目解答
答案
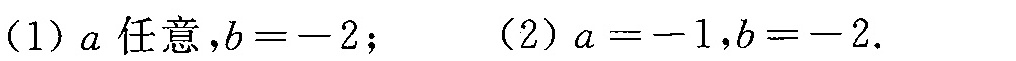
解析
步骤 1:求左极限
当$x<0$时,$f(x)=x^2-2$,因此$\lim_{x\to 0^-}f(x)=\lim_{x\to 0^-}(x^2-2)=-2$。
步骤 2:求右极限
当$x>0$时,$f(x)=\dfrac{\ln(1+bx)}{x}$,因此$\lim_{x\to 0^+}f(x)=\lim_{x\to 0^+}\dfrac{\ln(1+bx)}{x}$。利用洛必达法则,$\lim_{x\to 0^+}\dfrac{\ln(1+bx)}{x}=\lim_{x\to 0^+}\dfrac{b}{1+bx}=b$。
步骤 3:求极限存在条件
要使$f(x)$在$x=0$处存在极限,必须满足$\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)$,即$-2=b$,因此$b=-2$。
步骤 4:求连续条件
要使$f(x)$在$x=0$处连续,必须满足$\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=f(0)$,即$-2=b=a-1$,因此$a=-1$,$b=-2$。
当$x<0$时,$f(x)=x^2-2$,因此$\lim_{x\to 0^-}f(x)=\lim_{x\to 0^-}(x^2-2)=-2$。
步骤 2:求右极限
当$x>0$时,$f(x)=\dfrac{\ln(1+bx)}{x}$,因此$\lim_{x\to 0^+}f(x)=\lim_{x\to 0^+}\dfrac{\ln(1+bx)}{x}$。利用洛必达法则,$\lim_{x\to 0^+}\dfrac{\ln(1+bx)}{x}=\lim_{x\to 0^+}\dfrac{b}{1+bx}=b$。
步骤 3:求极限存在条件
要使$f(x)$在$x=0$处存在极限,必须满足$\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)$,即$-2=b$,因此$b=-2$。
步骤 4:求连续条件
要使$f(x)$在$x=0$处连续,必须满足$\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=f(0)$,即$-2=b=a-1$,因此$a=-1$,$b=-2$。