题目
设'((x)^2)=dfrac (1)(x) ( x > 0 ) ,则 f ( x ) = _____.
设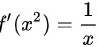
( x > 0 ) ,则 f ( x ) = _____.
题目解答
答案
解：因为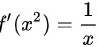 ( x > 0 ) ,
所以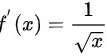
,
所以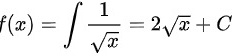
(C为常数)
故答案为：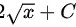
解析
步骤 1：理解给定条件
给定条件是$f'({x}^{2})=\dfrac {1}{x}$，其中$x > 0$。这意味着函数$f$的导数在$x^2$处的值等于$\dfrac {1}{x}$。
步骤 2：求解$f'(x)$
为了求解$f(x)$，我们首先需要求解$f'(x)$。由于$f'({x}^{2})=\dfrac {1}{x}$，我们可以通过变量替换来求解$f'(x)$。令$u = x^2$，则$x = \sqrt{u}$，因此$f'(u) = \dfrac{1}{\sqrt{u}}$。所以$f'(x) = \dfrac{1}{\sqrt{x}}$。
步骤 3：求解$f(x)$
现在我们知道了$f'(x) = \dfrac{1}{\sqrt{x}}$，我们可以通过积分求解$f(x)$。即$f(x) = \int \dfrac{1}{\sqrt{x}} dx$。积分结果为$f(x) = 2\sqrt{x} + C$，其中$C$是积分常数。
给定条件是$f'({x}^{2})=\dfrac {1}{x}$，其中$x > 0$。这意味着函数$f$的导数在$x^2$处的值等于$\dfrac {1}{x}$。
步骤 2：求解$f'(x)$
为了求解$f(x)$，我们首先需要求解$f'(x)$。由于$f'({x}^{2})=\dfrac {1}{x}$，我们可以通过变量替换来求解$f'(x)$。令$u = x^2$，则$x = \sqrt{u}$，因此$f'(u) = \dfrac{1}{\sqrt{u}}$。所以$f'(x) = \dfrac{1}{\sqrt{x}}$。
步骤 3：求解$f(x)$
现在我们知道了$f'(x) = \dfrac{1}{\sqrt{x}}$，我们可以通过积分求解$f(x)$。即$f(x) = \int \dfrac{1}{\sqrt{x}} dx$。积分结果为$f(x) = 2\sqrt{x} + C$，其中$C$是积分常数。