题目
1.-|||-若limf(x)存在,且 (x)=(x)^3+dfrac (2{x)^2+1}(x+1)+2lim _(xarrow 1)f(x) ,则 lim _(xarrow 1)f(x)= __ .
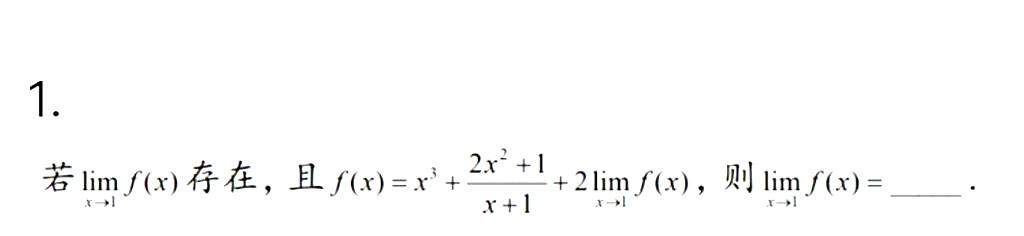
题目解答
答案

解析
步骤 1:确定极限存在
由于题目中提到 $\lim _{x\rightarrow 1}f(x)$ 存在,我们可以设 $\lim _{x\rightarrow 1}f(x)=a$,其中 $a$ 是一个常数。
步骤 2:代入极限值
将 $f(x)$ 的表达式代入 $\lim _{x\rightarrow 1}f(x)$,得到:
$$
\lim _{x\rightarrow 1}f(x) = \lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}+2\lim _{x\rightarrow 1}f(x)\right)
$$
由于 $\lim _{x\rightarrow 1}f(x)=a$,则有:
$$
a = \lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}+2a\right)
$$
步骤 3:计算极限
计算 $\lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}\right)$:
$$
\lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}\right) = 1^3 + \dfrac{2\cdot1^2+1}{1+1} = 1 + \dfrac{3}{2} = \dfrac{5}{2}
$$
因此,我们有:
$$
a = \dfrac{5}{2} + 2a
$$
步骤 4:求解 $a$
解方程 $a = \dfrac{5}{2} + 2a$,得到:
$$
a - 2a = \dfrac{5}{2}
$$
$$
-a = \dfrac{5}{2}
$$
$$
a = -\dfrac{5}{2}
$$
由于题目中提到 $\lim _{x\rightarrow 1}f(x)$ 存在,我们可以设 $\lim _{x\rightarrow 1}f(x)=a$,其中 $a$ 是一个常数。
步骤 2:代入极限值
将 $f(x)$ 的表达式代入 $\lim _{x\rightarrow 1}f(x)$,得到:
$$
\lim _{x\rightarrow 1}f(x) = \lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}+2\lim _{x\rightarrow 1}f(x)\right)
$$
由于 $\lim _{x\rightarrow 1}f(x)=a$,则有:
$$
a = \lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}+2a\right)
$$
步骤 3:计算极限
计算 $\lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}\right)$:
$$
\lim _{x\rightarrow 1}\left({x}^{3}+\dfrac {2{x}^{2}+1}{x+1}\right) = 1^3 + \dfrac{2\cdot1^2+1}{1+1} = 1 + \dfrac{3}{2} = \dfrac{5}{2}
$$
因此,我们有:
$$
a = \dfrac{5}{2} + 2a
$$
步骤 4:求解 $a$
解方程 $a = \dfrac{5}{2} + 2a$,得到:
$$
a - 2a = \dfrac{5}{2}
$$
$$
-a = \dfrac{5}{2}
$$
$$
a = -\dfrac{5}{2}
$$