题目
设 y=f(x) 的反函数是 =varphi (y), 且 (x)=(int )_(1)^2x(e)^(t^2)dt+1, 则 varphi '(1)=. __
题目解答
答案
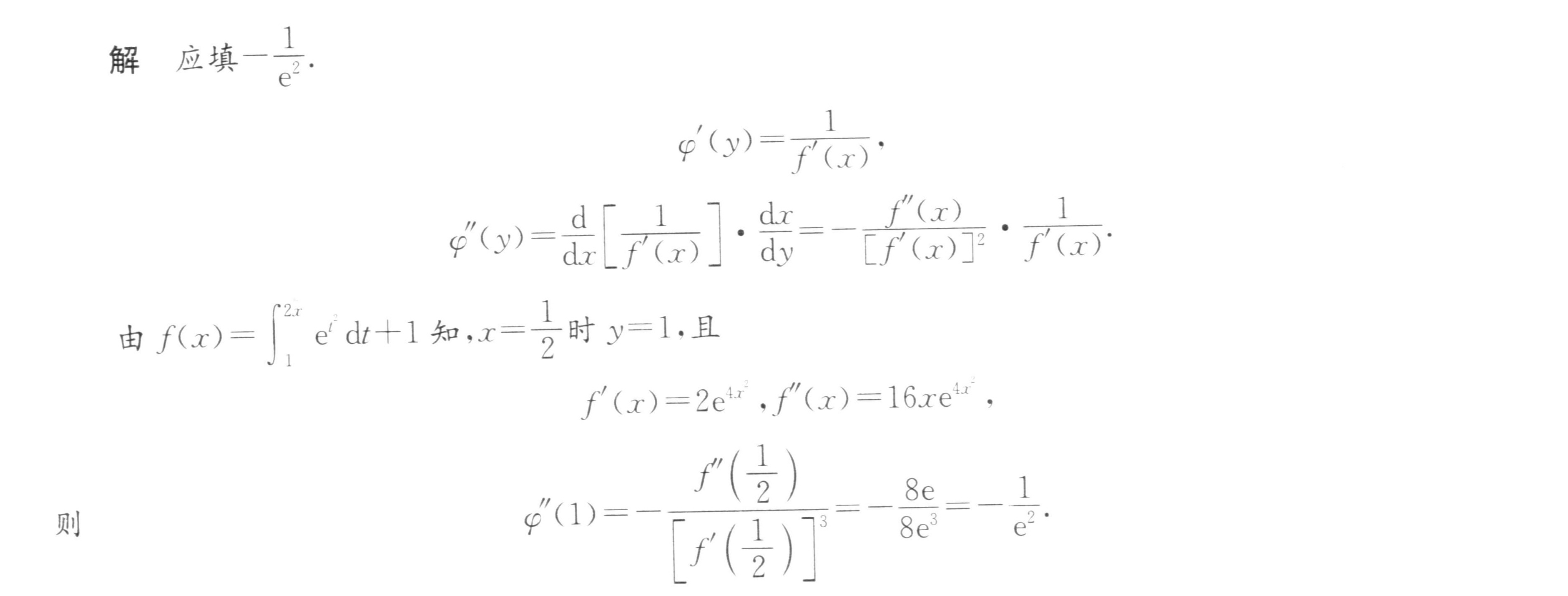
解析
步骤 1:求导数
首先,我们需要求出函数 $f(x)$ 的一阶导数 $f'(x)$ 和二阶导数 $f''(x)$。根据题目,$f(x)={\int }_{1}^{2x}{e}^{{t}^{2}}dt+1$。利用微积分基本定理,我们有:
$$f'(x) = \frac{d}{dx} \left( {\int }_{1}^{2x}{e}^{{t}^{2}}dt \right) = 2e^{(2x)^2} = 2e^{4x^2}$$
步骤 2:求反函数的导数
根据反函数的导数公式,我们有:
$$\varphi'(y) = \frac{1}{f'(x)}$$
步骤 3:求反函数的二阶导数
根据反函数的二阶导数公式,我们有:
$$\varphi''(y) = \frac{d}{dx} \left( \frac{1}{f'(x)} \right) \cdot \frac{dx}{dy} = -\frac{f''(x)}{[f'(x)]^2} \cdot \frac{1}{f'(x)}$$
步骤 4:计算 $\varphi''(1)$
当 $y=1$ 时,$x=\frac{1}{2}$,因此我们需要计算 $f''(x)$ 在 $x=\frac{1}{2}$ 时的值。根据步骤 1,我们有:
$$f''(x) = \frac{d}{dx} \left( 2e^{4x^2} \right) = 16xe^{4x^2}$$
因此,$f''(\frac{1}{2}) = 16 \cdot \frac{1}{2} \cdot e^{4 \cdot (\frac{1}{2})^2} = 8e$。将 $f'(x)$ 和 $f''(x)$ 的值代入步骤 3 的公式中,我们得到:
$$\varphi''(1) = -\frac{8e}{(2e)^3} = -\frac{8e}{8e^3} = -\frac{1}{e^2}$$
首先,我们需要求出函数 $f(x)$ 的一阶导数 $f'(x)$ 和二阶导数 $f''(x)$。根据题目,$f(x)={\int }_{1}^{2x}{e}^{{t}^{2}}dt+1$。利用微积分基本定理,我们有:
$$f'(x) = \frac{d}{dx} \left( {\int }_{1}^{2x}{e}^{{t}^{2}}dt \right) = 2e^{(2x)^2} = 2e^{4x^2}$$
步骤 2:求反函数的导数
根据反函数的导数公式,我们有:
$$\varphi'(y) = \frac{1}{f'(x)}$$
步骤 3:求反函数的二阶导数
根据反函数的二阶导数公式,我们有:
$$\varphi''(y) = \frac{d}{dx} \left( \frac{1}{f'(x)} \right) \cdot \frac{dx}{dy} = -\frac{f''(x)}{[f'(x)]^2} \cdot \frac{1}{f'(x)}$$
步骤 4:计算 $\varphi''(1)$
当 $y=1$ 时,$x=\frac{1}{2}$,因此我们需要计算 $f''(x)$ 在 $x=\frac{1}{2}$ 时的值。根据步骤 1,我们有:
$$f''(x) = \frac{d}{dx} \left( 2e^{4x^2} \right) = 16xe^{4x^2}$$
因此,$f''(\frac{1}{2}) = 16 \cdot \frac{1}{2} \cdot e^{4 \cdot (\frac{1}{2})^2} = 8e$。将 $f'(x)$ 和 $f''(x)$ 的值代入步骤 3 的公式中,我们得到:
$$\varphi''(1) = -\frac{8e}{(2e)^3} = -\frac{8e}{8e^3} = -\frac{1}{e^2}$$