题目
给定向量组α1=(1,-2,3,-1,2)T,α2=(3,-1,5,-3,1)T,α3=(5,0,7,-5,-4)T,α4=(2,1,2,-2,-3)T,求: (1)此向量组的秩; (2)此向量组的一个极大无关组; (3)判定此向量组的线性相关性; (4)将向量组的其他向量用求出的极大无关组线性表示.
给定向量组α1=(1,-2,3,-1,2)T,α2=(3,-1,5,-3,1)T,α3=(5,0,7,-5,-4)T,α4=(2,1,2,-2,-3)T,求:
(1)此向量组的秩;
(2)此向量组的一个极大无关组;
(3)判定此向量组的线性相关性;
(4)将向量组的其他向量用求出的极大无关组线性表示.
题目解答
答案
对以α1,α2,α3,α4为列向量的矩阵A作初等行变换,
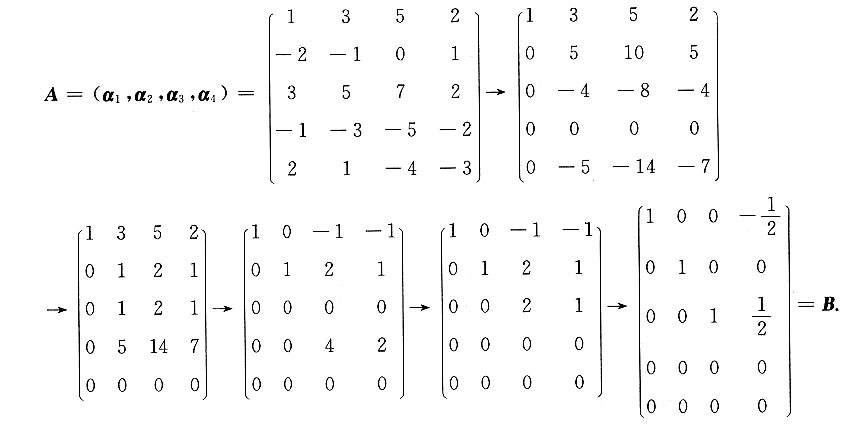
(1)r(α1,α2,α3,α4)=r(A)=r(B)=3;
(2)α1,α2,α3是向量组的一个极大无关组;
(3)α1,α2,α3,α4线性相关;
(4)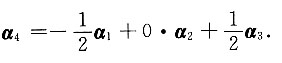

(1)r(α1,α2,α3,α4)=r(A)=r(B)=3;
(2)α1,α2,α3是向量组的一个极大无关组;
(3)α1,α2,α3,α4线性相关;
(4)
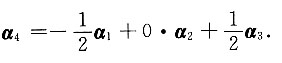
解析
考查要点:本题主要考查向量组的秩、极大无关组、线性相关性及线性表示的求解方法,核心是通过矩阵的初等行变换进行分析。
解题思路:
- 构造矩阵:将向量组作为列向量组成矩阵$A$。
- 行简化阶梯形:对矩阵$A$进行初等行变换,化为行最简形矩阵$B$。
- 确定秩:非零行的数量即为向量组的秩。
- 极大无关组:主元所在列对应的原向量构成极大无关组。
- 线性相关性:若秩小于向量个数,则向量组线性相关。
- 线性表示:通过行简化矩阵中非主元列的系数,将对应向量用极大无关组表示。
关键点:正确进行矩阵的行变换,准确识别主元位置及非主元列的系数。
第(1)题:求向量组的秩
-
构造矩阵:将$\alpha_1, \alpha_2, \alpha_3, \alpha_4$作为列向量组成矩阵$A$:
$A = \begin{pmatrix} 1 & 3 & 5 & 2 \\ -2 & -1 & 0 & 1 \\ 3 & 5 & 7 & -4 \\ -1 & -3 & -5 & -2 \\ 2 & 1 & -4 & -3 \end{pmatrix}$ -
行简化阶梯形:通过初等行变换,矩阵$A$化为:
$B = \begin{pmatrix} 1 & 0 & 0 & -\frac{1}{2} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \frac{1}{2} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ -
确定秩:非零行有3行,因此秩$r(A) = 3$。
第(2)题:求极大无关组
- 主元位置:行简化矩阵$B$中主元位于第1、2、3列。
- 对应原向量:因此极大无关组为$\alpha_1, \alpha_2, \alpha_3$。
第(3)题:判定线性相关性
- 秩与向量个数:向量组有4个向量,秩为3,小于向量个数。
- 结论:向量组线性相关。
第(4)题:用极大无关组表示其他向量
- 非主元列分析:第4列对应方程:
$\alpha_4 = -\frac{1}{2}\alpha_1 + 0 \cdot \alpha_2 + \frac{1}{2}\alpha_3$