题目
设矩阵d`v均为d`v阶方阵,若d`v与d`v同解,则( ).d`v仅有零解 d`v仅有零解 d`v与d`v同解 d`v与d`v同解
设矩阵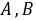 均为
均为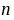 阶方阵,若
阶方阵,若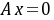 与
与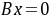 同解,则( ).
同解,则( ).
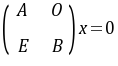 仅有零解
仅有零解
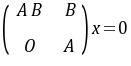 仅有零解
仅有零解
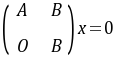 与
与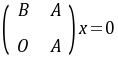 同解
同解
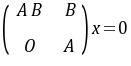 与
与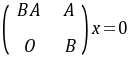 同解
同解
题目解答
答案
最佳答案
[答案]C
解析
考查要点:本题主要考查齐次线性方程组同解的条件,以及矩阵乘积的零空间关系。
解题核心思路:
若齐次方程组 $AX=0$ 与 $BX=0$ 同解,则它们的解空间完全相同,即 $A$ 和 $B$ 的零空间相同。进一步分析矩阵乘积 $AB$ 和 $BA$ 的零空间关系,利用 矩阵乘积的秩性质 和 零空间包含关系,推导出 $ABX=0$ 与 $BA X=0$ 的解空间是否相同。
破题关键点:
- 同解方程组的零空间相等:$N(A) = N(B)$。
- 矩阵乘积的零空间关系:若 $X \in N(A)$,则 $ABX = A(BX) = A \cdot 0 = 0$,同理若 $X \in N(B)$,则 $BA X = B(A X) = B \cdot 0 = 0$。
- 结论:$ABX=0$ 和 $BA X=0$ 的解空间均为 $N(A) = N(B)$,因此两者同解。
关键步骤分析:
-
同解方程组的性质:
已知 $AX=0$ 与 $BX=0$ 同解,说明它们的解空间完全相同,即 $A$ 和 $B$ 的零空间相等,即 $N(A) = N(B)$。 -
分析 $ABX=0$ 的解空间:
- 若 $X \in N(A)$,则 $AX=0$,因此 $ABX = A(BX) = A \cdot 0 = 0$,即 $X$ 是 $ABX=0$ 的解。
- 反之,若 $ABX=0$,则 $B X \in N(A)$,即 $B X \in N(B)$(因 $N(A)=N(B)$),故 $B X = 0$,从而 $X \in N(B) = N(A)$。
- 因此,$ABX=0$ 的解空间为 $N(A) = N(B)$。
-
分析 $BA X=0$ 的解空间:
- 若 $X \in N(B)$,则 $BX=0$,因此 $BA X = B(A X) = B \cdot 0 = 0$,即 $X$ 是 $BA X=0$ 的解。
- 反之,若 $BA X=0$,则 $A X \in N(B)$,即 $A X \in N(A)$(因 $N(A)=N(B)$),故 $A X = 0$,从而 $X \in N(A) = N(B)$。
- 因此,$BA X=0$ 的解空间也为 $N(A) = N(B)$。
-
结论:
$ABX=0$ 与 $BA X=0$ 的解空间完全相同,故两者同解。