题目
设f(x)= {x)^3,xleqslant 1 (x)^2,xgt 1 . 则f(x)在 x=1 处的
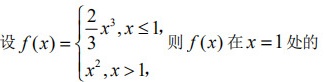

题目解答
答案
解析:
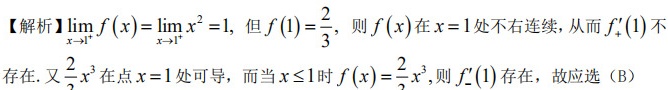
解析
步骤 1:计算右导数
首先,我们计算函数在 x=1 处的右导数。由于当 x>1 时,f(x)=x^2,因此右导数为:
\[f'(1^+)=\lim_{x\to1^+}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1^+}\frac{x^2-\frac{2}{3}}{x-1}\]
由于f(1)在x=1处的值为\(\frac{2}{3}\),因此右导数不存在,因为函数在x=1处不连续。
步骤 2:计算左导数
接下来,我们计算函数在 x=1 处的左导数。由于当 x≤1 时,f(x)=\(\frac{2}{3}x^3\),因此左导数为:
\[f'(1^-)=\lim_{x\to1^-}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1^-}\frac{\frac{2}{3}x^3-\frac{2}{3}}{x-1}\]
\[=\lim_{x\to1^-}\frac{2}{3}\frac{x^3-1}{x-1}=\lim_{x\to1^-}\frac{2}{3}(x^2+x+1)=2\]
因此,左导数存在且等于2。
步骤 3:结论
综上所述,f(x)在 x=1 处的左导数存在,但右导数不存在。
首先,我们计算函数在 x=1 处的右导数。由于当 x>1 时,f(x)=x^2,因此右导数为:
\[f'(1^+)=\lim_{x\to1^+}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1^+}\frac{x^2-\frac{2}{3}}{x-1}\]
由于f(1)在x=1处的值为\(\frac{2}{3}\),因此右导数不存在,因为函数在x=1处不连续。
步骤 2:计算左导数
接下来,我们计算函数在 x=1 处的左导数。由于当 x≤1 时,f(x)=\(\frac{2}{3}x^3\),因此左导数为:
\[f'(1^-)=\lim_{x\to1^-}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1^-}\frac{\frac{2}{3}x^3-\frac{2}{3}}{x-1}\]
\[=\lim_{x\to1^-}\frac{2}{3}\frac{x^3-1}{x-1}=\lim_{x\to1^-}\frac{2}{3}(x^2+x+1)=2\]
因此,左导数存在且等于2。
步骤 3:结论
综上所述,f(x)在 x=1 处的左导数存在,但右导数不存在。