题目
求int dfrac (dx)(1+sqrt [3]{x+1)}.
求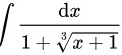 .
.
题目解答
答案
作变量代换: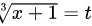 ,则
,则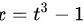 ,
,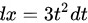 .代入
.代入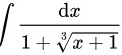 可得:
可得:
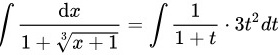
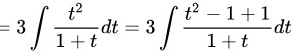
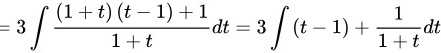
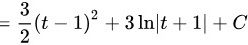 .
.
将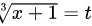 代入可得:
代入可得:
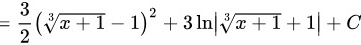
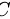 是任意常数.
是任意常数.
解析
步骤 1:变量代换
令$\sqrt [3]{x+1}=t$,则$x=t^3-1$,$dx=3t^2dt$。代入原积分可得:
$\int \dfrac {dx}{1+\sqrt [3]{x+1}}=\int \dfrac {1}{1+t}\cdot 3t^2dt$。
步骤 2:化简积分
$3\int \dfrac {t^2}{1+t}dt=3\int \dfrac {t^2-1+1}{1+t}dt$。
步骤 3:分部积分
$3\int \dfrac {(1+t)(t-1)+1}{1+t}dt=3\int (t-1)+\dfrac {1}{1+t}dt$。
步骤 4:计算积分
$=\dfrac {3}{2}{(t-1)}^{2}+3\ln |t+1|+C$。
步骤 5:回代变量
将$\sqrt [3]{x+1}=t$代入可得:
$=\dfrac {3}{2}{(\sqrt [3]{x+1}-1)}^{2}+3\ln |\sqrt [3]{x+1}+1|+C$。
令$\sqrt [3]{x+1}=t$,则$x=t^3-1$,$dx=3t^2dt$。代入原积分可得:
$\int \dfrac {dx}{1+\sqrt [3]{x+1}}=\int \dfrac {1}{1+t}\cdot 3t^2dt$。
步骤 2:化简积分
$3\int \dfrac {t^2}{1+t}dt=3\int \dfrac {t^2-1+1}{1+t}dt$。
步骤 3:分部积分
$3\int \dfrac {(1+t)(t-1)+1}{1+t}dt=3\int (t-1)+\dfrac {1}{1+t}dt$。
步骤 4:计算积分
$=\dfrac {3}{2}{(t-1)}^{2}+3\ln |t+1|+C$。
步骤 5:回代变量
将$\sqrt [3]{x+1}=t$代入可得:
$=\dfrac {3}{2}{(\sqrt [3]{x+1}-1)}^{2}+3\ln |\sqrt [3]{x+1}+1|+C$。