题目
.int dfrac (1+{cos )^2x}(1+cos 2x)dx
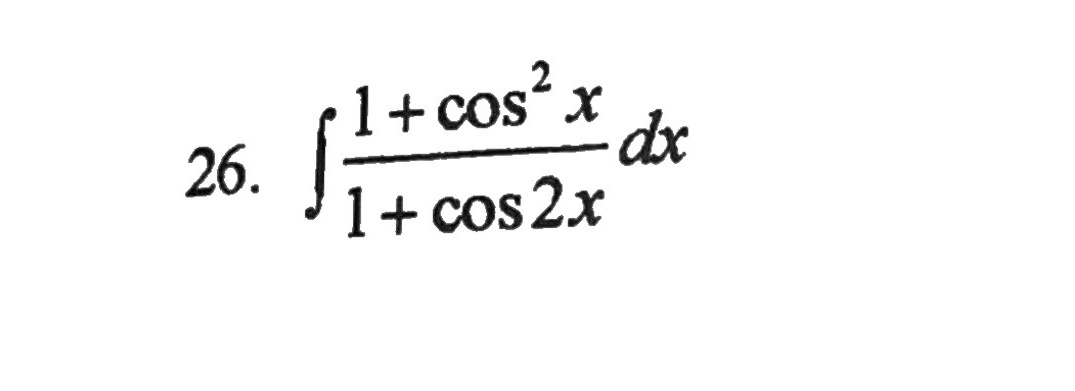
题目解答
答案

解析
步骤 1:化简被积函数
首先,我们注意到分母中的 $\cos 2x$ 可以用二倍角公式 $\cos 2x = 2\cos^2 x - 1$ 来替换。因此,分母可以写为 $1 + \cos 2x = 1 + 2\cos^2 x - 1 = 2\cos^2 x$。所以,原积分可以写为:
$$\int \dfrac {1+{\cos }^{2}x}{2{\cos }^{2}x}dx$$
步骤 2:分离被积函数
将被积函数分离为两个部分:
$$\int \left(\dfrac {1}{2{\cos }^{2}x} + \dfrac {{\cos }^{2}x}{2{\cos }^{2}x}\right)dx$$
步骤 3:积分
对分离后的两个部分分别积分:
$$\int \dfrac {1}{2{\cos }^{2}x}dx + \int \dfrac {1}{2}dx$$
第一个积分可以写为 $\dfrac{1}{2}\int \sec^2 x dx$,我们知道 $\int \sec^2 x dx = \tan x + C$,所以第一个积分的结果是 $\dfrac{1}{2}\tan x + C$。第二个积分是 $\dfrac{1}{2}x + C$。将两个结果相加,得到最终答案。
首先,我们注意到分母中的 $\cos 2x$ 可以用二倍角公式 $\cos 2x = 2\cos^2 x - 1$ 来替换。因此,分母可以写为 $1 + \cos 2x = 1 + 2\cos^2 x - 1 = 2\cos^2 x$。所以,原积分可以写为:
$$\int \dfrac {1+{\cos }^{2}x}{2{\cos }^{2}x}dx$$
步骤 2:分离被积函数
将被积函数分离为两个部分:
$$\int \left(\dfrac {1}{2{\cos }^{2}x} + \dfrac {{\cos }^{2}x}{2{\cos }^{2}x}\right)dx$$
步骤 3:积分
对分离后的两个部分分别积分:
$$\int \dfrac {1}{2{\cos }^{2}x}dx + \int \dfrac {1}{2}dx$$
第一个积分可以写为 $\dfrac{1}{2}\int \sec^2 x dx$,我们知道 $\int \sec^2 x dx = \tan x + C$,所以第一个积分的结果是 $\dfrac{1}{2}\tan x + C$。第二个积分是 $\dfrac{1}{2}x + C$。将两个结果相加,得到最终答案。