题目
4.设函数 (x)=dfrac ({2)^x}(1+x) 则 [ f(0)] = 【() 】.-|||-A.0 B.1 C. -1 D.2

题目解答
答案
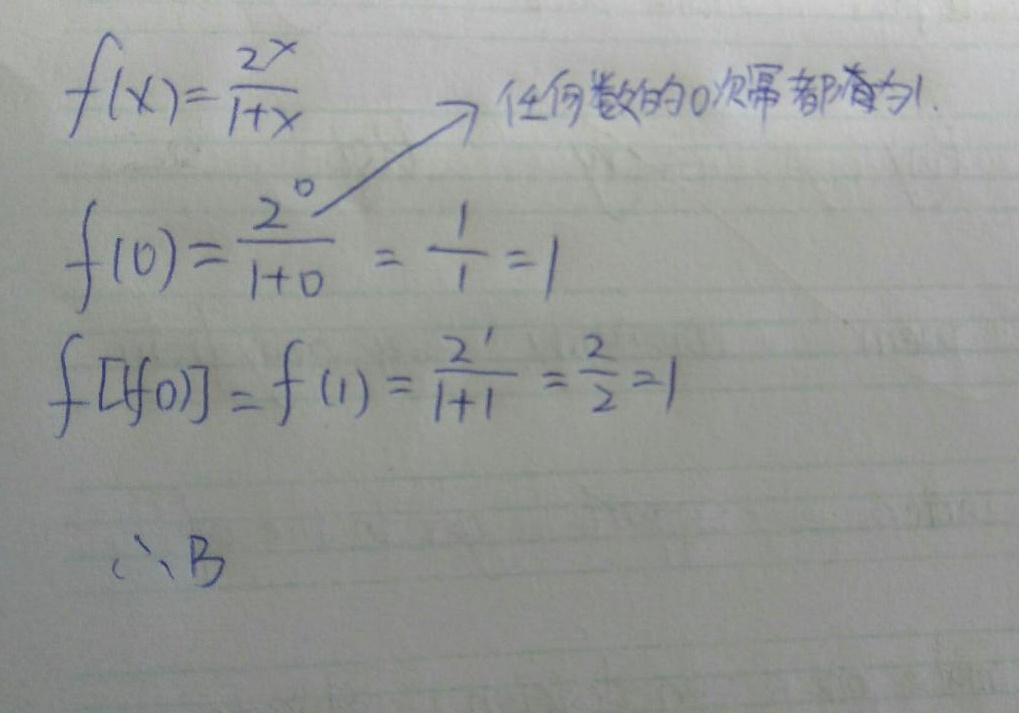
解析
步骤 1:计算 $f(0)$
根据函数 $f(x)=\dfrac {{2}^{x}}{1+x}$,将 $x=0$ 代入,得到 $f(0)=\dfrac {{2}^{0}}{1+0}=\dfrac {1}{1}=1$。
步骤 2:计算 $f[f(0)]$
由于 $f(0)=1$,则 $f[f(0)]=f(1)$。将 $x=1$ 代入函数 $f(x)$,得到 $f(1)=\dfrac {{2}^{1}}{1+1}=\dfrac {2}{2}=1$。
根据函数 $f(x)=\dfrac {{2}^{x}}{1+x}$,将 $x=0$ 代入,得到 $f(0)=\dfrac {{2}^{0}}{1+0}=\dfrac {1}{1}=1$。
步骤 2:计算 $f[f(0)]$
由于 $f(0)=1$,则 $f[f(0)]=f(1)$。将 $x=1$ 代入函数 $f(x)$,得到 $f(1)=\dfrac {{2}^{1}}{1+1}=\dfrac {2}{2}=1$。