题目
求极限lim _(xarrow {0)^+}dfrac (1-sqrt {cos x)}(x(1-cos sqrt {x))}
求极限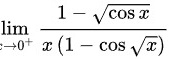
题目解答
答案
进行一次有理化,分子分母同时乘以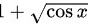 有:
有:
极限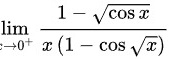
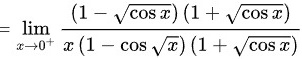
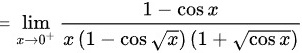
根据等价无穷小,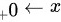 时,
时,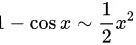
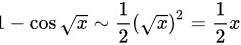
∴
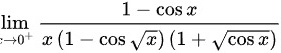
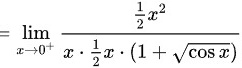
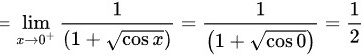
所以本题答案为极限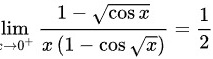
解析
步骤 1:有理化分子
为了消除根号,我们对分子和分母同时乘以$1+\sqrt {\cos x}$,这样可以利用差平方公式$(a-b)(a+b)=a^2-b^2$来简化表达式。
步骤 2:应用等价无穷小
当$x$趋近于$0$时,$1-\cos x$可以近似为$\dfrac{1}{2}x^2$,这是由于$\cos x$在$x=0$处的泰勒展开式为$1-\dfrac{1}{2}x^2+O(x^4)$。同样地,$1-\cos \sqrt{x}$可以近似为$\dfrac{1}{2}x$,因为$\cos \sqrt{x}$在$x=0$处的泰勒展开式为$1-\dfrac{1}{2}x+O(x^2)$。
步骤 3:计算极限
将上述等价无穷小代入原式,然后计算极限。
为了消除根号,我们对分子和分母同时乘以$1+\sqrt {\cos x}$,这样可以利用差平方公式$(a-b)(a+b)=a^2-b^2$来简化表达式。
步骤 2:应用等价无穷小
当$x$趋近于$0$时,$1-\cos x$可以近似为$\dfrac{1}{2}x^2$,这是由于$\cos x$在$x=0$处的泰勒展开式为$1-\dfrac{1}{2}x^2+O(x^4)$。同样地,$1-\cos \sqrt{x}$可以近似为$\dfrac{1}{2}x$,因为$\cos \sqrt{x}$在$x=0$处的泰勒展开式为$1-\dfrac{1}{2}x+O(x^2)$。
步骤 3:计算极限
将上述等价无穷小代入原式,然后计算极限。