题目
[题目]求导数: =ln (x+sqrt (1+{x)^2})
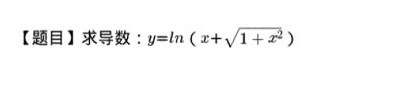
题目解答
答案

解析
步骤 1:确定函数形式
给定函数 $y=\ln (x+\sqrt {1+{x}^{2}})$,这是一个复合函数,其中外层函数是自然对数函数,内层函数是 $x+\sqrt {1+{x}^{2}}$。
步骤 2:应用链式法则
根据链式法则,复合函数的导数等于外层函数的导数乘以内层函数的导数。因此,我们需要分别求出外层函数和内层函数的导数。
步骤 3:求外层函数的导数
外层函数是自然对数函数 $\ln(u)$,其导数为 $\frac{1}{u}$,其中 $u=x+\sqrt {1+{x}^{2}}$。
步骤 4:求内层函数的导数
内层函数是 $x+\sqrt {1+{x}^{2}}$,其导数为 $1+\frac{x}{\sqrt{1+x^2}}$,这是通过求导 $x$ 和 $\sqrt{1+x^2}$ 并相加得到的。
步骤 5:应用链式法则
将外层函数的导数和内层函数的导数相乘,得到 $y'$ 的表达式。即 $y'=\frac{1}{x+\sqrt{1+x^2}} \cdot (1+\frac{x}{\sqrt{1+x^2}})$。
步骤 6:简化表达式
将 $y'$ 的表达式简化,得到最终的导数表达式。$y'=\frac{1}{x+\sqrt{1+x^2}} \cdot \frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}} = \frac{1}{\sqrt{1+x^2}}$。
给定函数 $y=\ln (x+\sqrt {1+{x}^{2}})$,这是一个复合函数,其中外层函数是自然对数函数,内层函数是 $x+\sqrt {1+{x}^{2}}$。
步骤 2:应用链式法则
根据链式法则,复合函数的导数等于外层函数的导数乘以内层函数的导数。因此,我们需要分别求出外层函数和内层函数的导数。
步骤 3:求外层函数的导数
外层函数是自然对数函数 $\ln(u)$,其导数为 $\frac{1}{u}$,其中 $u=x+\sqrt {1+{x}^{2}}$。
步骤 4:求内层函数的导数
内层函数是 $x+\sqrt {1+{x}^{2}}$,其导数为 $1+\frac{x}{\sqrt{1+x^2}}$,这是通过求导 $x$ 和 $\sqrt{1+x^2}$ 并相加得到的。
步骤 5:应用链式法则
将外层函数的导数和内层函数的导数相乘,得到 $y'$ 的表达式。即 $y'=\frac{1}{x+\sqrt{1+x^2}} \cdot (1+\frac{x}{\sqrt{1+x^2}})$。
步骤 6:简化表达式
将 $y'$ 的表达式简化,得到最终的导数表达式。$y'=\frac{1}{x+\sqrt{1+x^2}} \cdot \frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}} = \frac{1}{\sqrt{1+x^2}}$。