题目
设p为常数,若反常积分 (int )_(0)^1dfrac (ln x)({x)^p((1-x))^1-p}dx 收敛,则p的取值范围是 () .-|||-(A) (-1,1) (B) (-1,2) (C) (-infty ,1) (D) (-infty ,2)
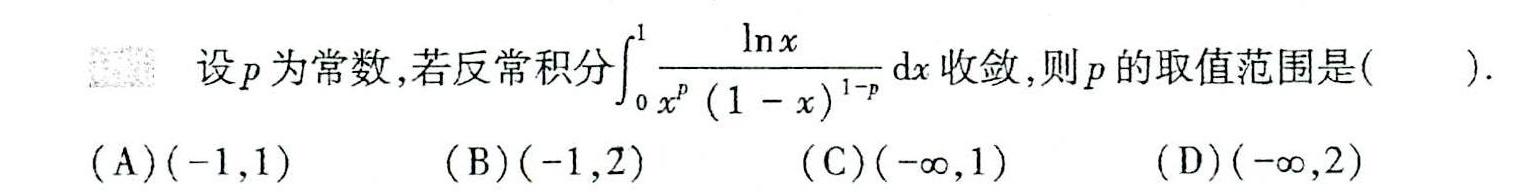
题目解答
答案

解析
步骤 1:分析积分的收敛性
反常积分 ${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-p}}dx$ 在 x=0 和 x=1 处有瑕点。我们需要分别分析这两个瑕点处积分的收敛性。
步骤 2:分析 x=0 处的积分收敛性
在 x=0 处,积分可以写为 ${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-p}}dx$。由于 $\ln x$ 在 x=0 处是无穷小量,而 ${x}^{p}$ 在 x=0 处是无穷大量,因此我们需要分析 ${x}^{p}$ 的幂次 p。当 $0 < p < 1$ 时,${x}^{p}$ 在 x=0 处是无穷大量,因此积分收敛。
步骤 3:分析 x=1 处的积分收敛性
在 x=1 处,积分可以写为 ${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-p}}dx$。由于 $\ln x$ 在 x=1 处是无穷小量,而 ${(1-x)}^{1-p}$ 在 x=1 处是无穷大量,因此我们需要分析 ${(1-x)}^{1-p}$ 的幂次 1-p。当 $0 < 1-p < 1$,即 $0 < p < 1$ 时,${(1-x)}^{1-p}$ 在 x=1 处是无穷大量,因此积分收敛。
步骤 4:综合分析
结合步骤 2 和步骤 3,我们发现当 $0 < p < 1$ 时,积分在 x=0 和 x=1 处都收敛。但是,我们还需要考虑 p=0 和 p=1 的情况。当 p=0 时,积分变为 ${\int }_{0}^{1}\dfrac {\ln x}{1-x}dx$,由于 $\lim _{x\rightarrow {1}^{-}}{(1-x)}^{\dfrac {1}{2}}\dfrac {\ln x}{1-x}=0$,所以积分收敛。当 p=1 时,积分变为 ${\int }_{0}^{1}\dfrac {\ln x}{x}dx$,由于 $\lim _{x\rightarrow {0}^{+}}{x}^{\dfrac {1}{2}}\dfrac {\ln x}{x}=0$,所以积分发散。因此,当 $-1 < p < 1$ 时,积分收敛。
反常积分 ${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-p}}dx$ 在 x=0 和 x=1 处有瑕点。我们需要分别分析这两个瑕点处积分的收敛性。
步骤 2:分析 x=0 处的积分收敛性
在 x=0 处,积分可以写为 ${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-p}}dx$。由于 $\ln x$ 在 x=0 处是无穷小量,而 ${x}^{p}$ 在 x=0 处是无穷大量,因此我们需要分析 ${x}^{p}$ 的幂次 p。当 $0 < p < 1$ 时,${x}^{p}$ 在 x=0 处是无穷大量,因此积分收敛。
步骤 3:分析 x=1 处的积分收敛性
在 x=1 处,积分可以写为 ${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-p}}dx$。由于 $\ln x$ 在 x=1 处是无穷小量,而 ${(1-x)}^{1-p}$ 在 x=1 处是无穷大量,因此我们需要分析 ${(1-x)}^{1-p}$ 的幂次 1-p。当 $0 < 1-p < 1$,即 $0 < p < 1$ 时,${(1-x)}^{1-p}$ 在 x=1 处是无穷大量,因此积分收敛。
步骤 4:综合分析
结合步骤 2 和步骤 3,我们发现当 $0 < p < 1$ 时,积分在 x=0 和 x=1 处都收敛。但是,我们还需要考虑 p=0 和 p=1 的情况。当 p=0 时,积分变为 ${\int }_{0}^{1}\dfrac {\ln x}{1-x}dx$,由于 $\lim _{x\rightarrow {1}^{-}}{(1-x)}^{\dfrac {1}{2}}\dfrac {\ln x}{1-x}=0$,所以积分收敛。当 p=1 时,积分变为 ${\int }_{0}^{1}\dfrac {\ln x}{x}dx$,由于 $\lim _{x\rightarrow {0}^{+}}{x}^{\dfrac {1}{2}}\dfrac {\ln x}{x}=0$,所以积分发散。因此,当 $-1 < p < 1$ 时,积分收敛。