设y=y(x)满足方程 y=y(x) 0 ) " data-width="252" data-height="33" data-size="2950" data-format="png" style="max-width:100%">且曲线y=y(x)有一斜渐近线为y=y(x)( I ) 求 y=y(x) ;( II ) 求y=y(x) 的极值
设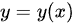 满足方程
满足方程 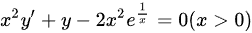 且曲线
且曲线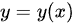 有一斜渐近线为
有一斜渐近线为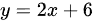
( I ) 求 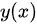 ;
;
( II ) 求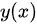 的极值
的极值
题目解答
答案
由题意,
题1:
对函数进行变形有
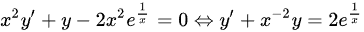
由一阶线性微分方程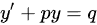 的通解公式
的通解公式
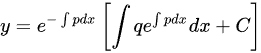
可求本题函数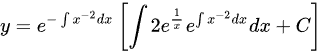
=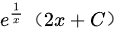
其次,由 曲线
曲线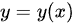 有一斜渐近线为
有一斜渐近线为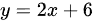
则得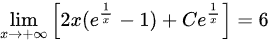
当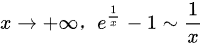
则得到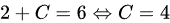
即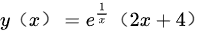
题2:
对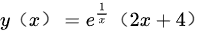 求导有
求导有
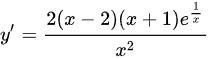
由于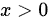 ,
,
可得极小值点有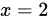 ,无极大值点
,无极大值点
因此有极小值为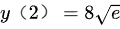
解析
考查要点:本题主要考查一阶线性微分方程的求解方法,以及利用渐近线条件确定特解,同时结合导数求极值。
解题思路:
- 微分方程求解:将原方程整理为标准形式,利用积分因子法求通解。
- 渐近线条件:通过斜渐近线方程确定通解中的常数,得到特解。
- 极值求解:对特解函数求导,分析导数的符号变化,确定极值点。
关键点:
- 积分因子的正确计算是解微分方程的核心。
- 渐近线条件的展开与极限分析需结合泰勒展开近似。
- 导数符号分析需注意分母和指数函数的正负性。
(I) 求 $y(x)$
1. 整理微分方程
原方程 $x^2 y' + y = 2x^2 e^{\frac{1}{x}}$,两边除以 $x^2$ 得标准形式:
$y' + \frac{1}{x^2} y = 2 e^{\frac{1}{x}}$
2. 计算积分因子
积分因子为:
$\mu(x) = e^{\int \frac{1}{x^2} dx} = e^{-\frac{1}{x}}$
3. 应用通解公式
通解为:
$y = e^{\frac{1}{x}} \left[ \int 2 e^{\frac{1}{x}} \cdot e^{-\frac{1}{x}} dx + C \right] = e^{\frac{1}{x}} (2x + C)$
4. 利用渐近线条件确定常数
当 $x \to +\infty$ 时,$e^{\frac{1}{x}} \sim 1 + \frac{1}{x}$,代入 $y = 2x + 6$:
$e^{\frac{1}{x}} (2x + C) - (2x + 6) \sim \left(2x + C + \frac{2x + C}{x}\right) - (2x + 6) = (C - 4) + \cdots = 0$
解得 $C = 4$,故特解为:
$y(x) = e^{\frac{1}{x}} (2x + 4)$
(II) 求 $y(x)$ 的极值
1. 求导数
$y'(x) = e^{\frac{1}{x}} \cdot \frac{2(x-2)(x+1)}{x^2}$
2. 分析导数符号
- 当 $0 < x < 2$ 时,$y'(x) < 0$;
- 当 $x > 2$ 时,$y'(x) > 0$。
3. 确定极值点
$x = 2$ 是极小值点,极小值为:
$y(2) = e^{\frac{1}{2}} \cdot 8 = 8\sqrt{e}$