题目
5.将函数 (x)=dfrac (1)(x) 展开成 (x-3) 的幂级数.
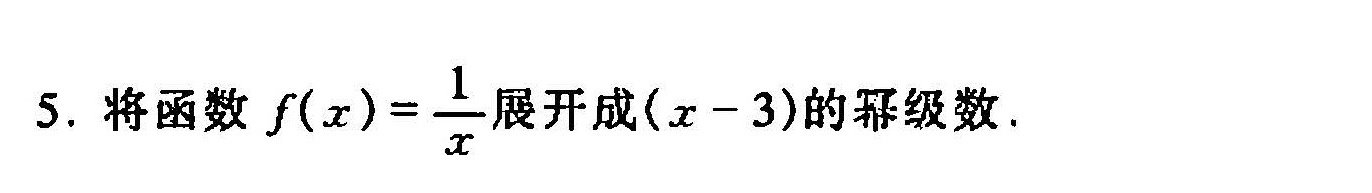
题目解答
答案
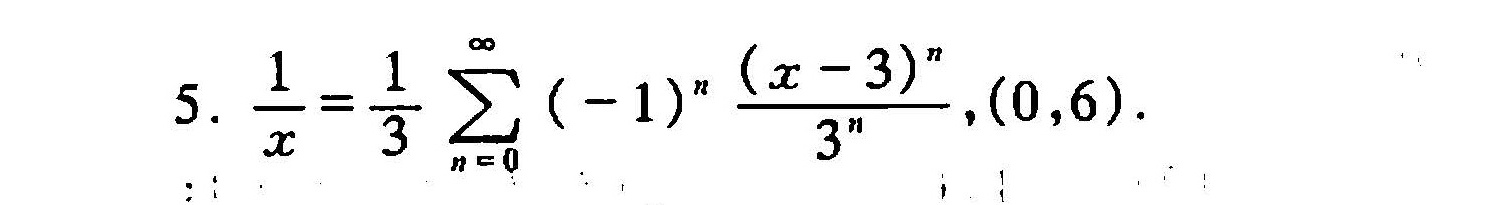
解析
步骤 1:将函数 $f(x)=\dfrac {1}{x}$ 转换为以 (x-3) 为变量的形式。
我们首先将 $f(x)$ 重写为 $\dfrac {1}{x}=\dfrac {1}{3+(x-3)}$,这样我们就可以将函数表示为以 (x-3) 为变量的形式。
步骤 2:将函数转换为几何级数的形式。
我们注意到 $\dfrac {1}{3+(x-3)}$ 可以写成 $\dfrac {1}{3}\cdot \dfrac {1}{1+\frac{x-3}{3}}$。由于 $\dfrac {1}{1+\frac{x-3}{3}}$ 可以表示为几何级数 $\sum _{n=0}^{\infty }{(-1)}^{n}\left(\frac{x-3}{3}\right)^{n}$,因此我们可以将原函数表示为几何级数的形式。
步骤 3:写出幂级数表达式。
将几何级数代入原函数,我们得到 $\dfrac {1}{x}=\dfrac {1}{3}\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-3)}^{n}}{{3}^{n}}$。这个表达式就是函数 $f(x)=\dfrac {1}{x}$ 关于 (x-3) 的幂级数展开式。
我们首先将 $f(x)$ 重写为 $\dfrac {1}{x}=\dfrac {1}{3+(x-3)}$,这样我们就可以将函数表示为以 (x-3) 为变量的形式。
步骤 2:将函数转换为几何级数的形式。
我们注意到 $\dfrac {1}{3+(x-3)}$ 可以写成 $\dfrac {1}{3}\cdot \dfrac {1}{1+\frac{x-3}{3}}$。由于 $\dfrac {1}{1+\frac{x-3}{3}}$ 可以表示为几何级数 $\sum _{n=0}^{\infty }{(-1)}^{n}\left(\frac{x-3}{3}\right)^{n}$,因此我们可以将原函数表示为几何级数的形式。
步骤 3:写出幂级数表达式。
将几何级数代入原函数,我们得到 $\dfrac {1}{x}=\dfrac {1}{3}\sum _{n=0}^{\infty }{(-1)}^{n}\dfrac {{(x-3)}^{n}}{{3}^{n}}$。这个表达式就是函数 $f(x)=\dfrac {1}{x}$ 关于 (x-3) 的幂级数展开式。